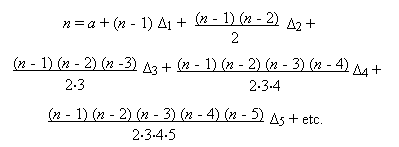The Swedish Tabulating Machine of G. & E. SCHEUTZ.

It is a well known fact that Mr. CHARLES E. BABBAGE was the first to attempt the construction of a Difference Engine; but owing to some misunderstanding between the inventor and the English government, under whose patronage the work was carried out, it was never completed.

In the Edinburgh Review for July, 1834, Dr. LARDNER gave an account of Mr. BABBAGE'S machine, which, coming under the eye of Mr. GEORGE SCHEUTZ, an eminent printer at Stockholm, he conceived the idea of building one which should do the work contemplated by Mr. BABBAGE, but on a totally different plan, as regards the details of the mechanism. After proving the practicability of his ideas in the construction of some models, it was allowed to rest for a year or two. In 1837, EDWARD, the son, took up the plan, and in conjunction with his father completed a machine of small compass in 1840. This was exhibited before the Swedish Academy of Sciences in 1843. On the certificate of that body, orders to manufacture machines were solicited in different countries, but without success. After numerous failures to secure assistance from the Swedish government, for the purpose of constructing a large and complete machine, finally in 1851, the Diet with difficulty consented to advance 5,000 rix-dollars, (about $1,500), on condition that the machine should be completed within a year, and that the inventors should give a guarantee to return that sum to the State if it did not prove successful.

Having already expended all their means in the construction of models and tools, they were unable to give the necessary guarantee, and the invention would probably have been abandoned, but for the noble liberality of fifteen members of the Swedish Academy of Sciences, who became responsible for the amount advanced.

The machine was completed in 1853, and performed its work perfectly. In consideration of the successful issue of the project, and the large sums that had been expended by the inventors, the Diet granted a reward of 5,000 rix-dollars, thus making the total grant 10,000 rix-dollars.

The machine was taken to England and exhibited before the Royal Society of London, and also placed in the great Paris Exposition, where the Gold Medal was unanimously awarded to the inventors.

It was purchased for the Dudley Observatory in 1856, at an expense of $5,000.

This machine was the only one built until 1863, when a duplicate was made for the Registrar General's Office, London, England.

This machine possesses a twofold power, with the mechanism appropriate for each; not necessarily connected, though simultaneous and automatic in its entire action. These functions are, first, the production of certain numerical results; second, the conversion of those results into a permanent legible record.

The theory of the machine is based on the mathematical truth, that in any series of numbers, the nth order of differences may be regarded as equal to zero, where n may be any number whatever. To produce such a series by mechanical means, the only condition necessary is that there be as many variable wheels indicating the numbers as we have differences. If n was a very large number, the mechanism would become cumbersome and unwieldly. It is found in practice that for the great majority of useful computations, four orders of differences are sufficient.

This machine is constructed for four orders, and will consequently compute any series, in which the fourth (or any inferior) order of differences are equal.

This will be more easily understood by a simple illustration. Suppose it is desired to tabulate the series of square numbers beginning with unity. Let us first see how these numbers can be produced by means of successive differences. We arrange them for convenience in the following table:

Number.	Square.	1st diff.	2d diff.	3d diff.
1	1
		3
2	4		2
		5		0
3	9		2
		7
4	16

Having given the number (1) square of 1, and the first difference 3 = (2² - 1²) and the second diff. 2 = (3² - 2²) - (2² - 1²), the squares of all successive numbers may be found by continued additions.

The difference between (2² - 1²) = 3 is the first diff.; the second diff. (2) is constant. Then,
  (3)² = 9 = (2)² + 1st diff.(3) + 2d diff.(2),
  or 9 = 4 + (3+2),
  or 9 = 4 + 5, (5) being the second number in column of first differences.

And the same process may be repeated to any extent.

What now is required in a machine, is, first to be able to produce the first order of differences, having given the first difference 3, and the second difference (2) constant.

Suppose we have a wheel, on the circumference of which is inscribed at equal distances apart, the numbers, 0, 1, 2, 3, 4, 5, 6, 7, 8 , 9. If this wheel should be set so that the figure 3 should coincide with a fixed mark, and by means of simple mechanism, it should be made to advance two

divisions at every motion of a lever, we should successively cause the numbers 3, 5, 7, 9, to coincide with the mark; and if when the wheel has made a complete revolution, it should cause another wheel placed by its side to advance one division, the process may be continued so as to form the series of first differences, in which every successive number would be greater by 2 than the number preceding.

This principle of successive additions is exemplified in an ordinary clock; for at every oscillation of the pendulum the second-hand advances one division, and after this has made a complete revolution, the minute-hand has also advanced one division. By a slight change in the escapement wheel, the second wheel could be made to advance 2, 3, or 4 divisions at every oscillation. Hence it will be readily understood how, by simple machinery, any constant quantity may be added.

Now suppose we have three wheels, placed one above the other on a vertical (shaft) axis, on each of which is inscribed zero and the nine digits, corresponding with a like number of divisions on their surfaces. If the number 1 on the upper wheel, 3 on the second wheel, and 2 on the third wheel, be brought opposite a fixed or zero point; and the nature of these wheels be such, that when set in motion by a lever from right to left, the second wheel adds its number to the upper wheel, and by a motion of the lever from left to right, the third wheel adds its number to the second (being in this case constant and always equal to 2); from this arrangement, we will be able to compute a table of square numbers.

We begin by moving the lever from right to left; when 3 (the number on the second wheel) will be added to 1 (the number on the upper wheel), making 4 the square of 2. On moving the lever back, 2 on the third wheel is added to 3 on the second wheel, making 5. Moving our lever back again from right to left, 5 is added to 4 on the upper wheel,

making 9, the square of 3. Repeating the process, we next get 7 on the second wheel; which added to 9 on the upper makes 16, the square of 4.

It is evident from the above statement that the series of squares is developed by a process of addition, in which the constant significant difference, increased by each preceding first difference, generates the order of first differences; and with the sum of the preceding first difference and square, produces the series of squares. This principle is true for any series, whatever number n may be.

It will now be readily understood, should we have a series of wheels, ranged under each other, the nature of which should be such that the series below should add its number to the one above, we could produce any series of numbers in which the fourth order of differences should be equal.

Plate IV is a perspective view of the machine drawn on a scale of 1/9 the full size.

The successive orders of differences are represented by Δ₀, Δ₁, Δ₂, Δ₃ and Δ₄. There are 15 vertical steel axles, each passing through five hollow rings of metal, on which are engraved 0 and the nine digits.

There is a groove cut around the circumference of each ring, by which it is supported on a small brass shelf; being

free to turn about its center horizontally in either direction. A perspective view of one of these rings is shown in fig. 1.

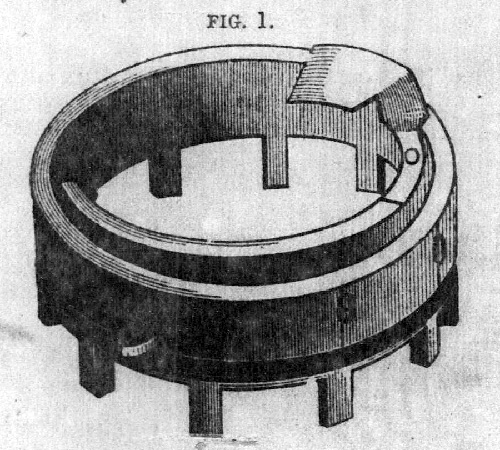
To each of the vertical axles is attached four brass shelves, fig. 2 supporting small steel levers mounted on pivots. These levers occupy a position directly underneath the rings (fig. 1) ; their office being to add to the ring above the number coinciding with the fixed mark engraved on the ring below.

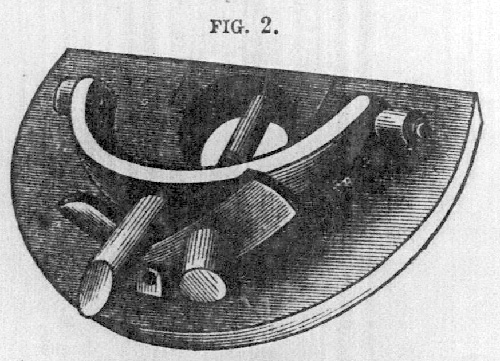
When the machine is put in operation by means of crank a, the lever b is moved out horizontally from right to left, causing every one of the vertical axles to revolve from right to left, thereby adding all the numbers on the row marked Δ₃ to those on Δ₂, and all those on Δ₁ to Δ₀. By continuing to turn the crank a, the lever b is moved back again from left to right, this time adding the number on Δ₄ to Δ₃, and those on Δ₂ to Δ₁. This process is continued long as the machine is kept in motion.

If we call the first axle to the right units, then the next one will represent tens, and the next hundreds, etc. The numbers on any row of differences is, therefore, read from left to right, as in ordinary writing.

When all the rings are set at zero, by making that division coincide with a fixed mark in front, no change will take place in their position when the machine is put in operation.

The process of carrying for 10 will best be understood by an example. Suppose all the rings in the first row Δ₀ be set

at zero, except the last one on the right hand, which we place at 5. Let all the rings on the second row Δ₁ be set at 9. If these numbers were written down they would stand thus:
  000 000 000 000 005 = Δ₀
  999 999 999 999 999 = Δ₁
Now when the lever b is moved from right to left, every number in Δ₁ will be added to Δ₀, and the result will stand thus:
  999 999 999 999 994 = Δ₀
It is readily perceived that the operation is not complete, since we ought to have
  Δ₀ = 000 000 000 000 004

When the 9 is added to 5, making 14, the units ring, in passing through zero, throws out a small lever (by means of the projection between the numbers 7 and 8 shown in fig. 1). As the motion of the machine is continued, the post c carrying a lever arm passes in front of the rings, and by means of the lever thrown out advances the second ring a unit, making it zero, it in turn throws out the next lever to the left, when the same process is repeated, and in this example all the rings on the upper row, except the 1st, is left at zero.

In case any difference is negative, we get the same result by adding the complement, or difference between the number and 10. Suppose we wish to subtract 2 from 3, our result would be 1. If we take the complement of 2 = 8, and add it to 3, we get (10 + 1), or the same result on the first wheel as before. If we wish to subtract
  000 000 000 142 346
we must set on the machine the complement of this number
  999 999 999 857 654
adding this complement is the same as subtracting the number itself.

By changing all the rings in the 3d and 5th vertical on the left, the computation can be made by the sexagesimal

system, that is, the results will at once be converted into degrees, minutes and seconds.

Before starting the machine for any computation, it is necessary to set the proper wheels, after which it needs no further attention; for so long as the last order of differences is constant, it will continue to produce the required numbers. Thus for producing a table of squares, it is only necessary to give the machine three numbers, 1, 3 and 2; and from these data we can compute the squares of all numbers up to 30 millions. In the same manner, by giving the machine the numbers 1, 7, 6, 6, we can produce a table of cubes, the limit being 15 figures. The same principles apply in the computation of logarithms, or any series of numbers whatever.

During the process of making the computation, the machine also prints the result, together with the proper argument, to 8 places of figures.

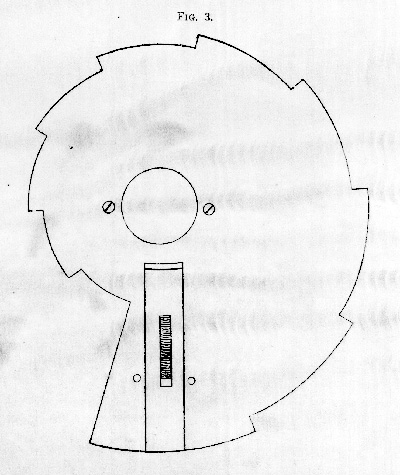
A portion of the mechanism for printing, is shown at the left end of plate IV. The numbers on the upper row of rings are transferred to the printing part, by means of "the snail" attached to and revolving with the upper rings. This contrivance shown in fig. 3, has long been used in the striking part of the common eight-day clock.

The results may be stereotyped on strips of lead, or printed on ordinary paper or card-board. By changing the position of the carrying post on one of the rings, we at once obtain the nearest whole number, no platter how many decimal places are used in the computation. At the average rate of working 120 complete results are calculated and printed in one hour.

In order to compute any series of numbers, it is necessary to determine the orders of differences belonging to that series, which must be set on the proper rings.

The general formula is:

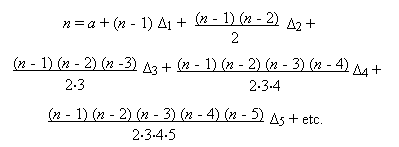
n = the number of the term.
a = the first term.
Δ₁, Δ₂, Δ₃, etc. = the orders of differences.
Then we have the following form of equations:

(n =   1) = a.
(n = 11) = a + 10Δ₁ +   45Δ₂ +   120Δ₃ +   210Δ₄ + etc.
(n = 21) = a + 20Δ₁ + 190Δ₂ + 1140Δ₃ + 4845Δ₄ + etc.
(n = 31) = a + 30Δ₁ + 435Δ₂ + 4060Δ₃ + 27405Δ₄ + etc.
(n = 41) = a + 40Δ₁ + 780Δ₂ + 9880Δ₃ + 91390Δ₄ + etc.

For facilitating the computation, the binomial co-efficients together with their logarithms, belonging to each order of differences, are tabulated up to 80 terms. The solution of the equations may also be abbreviated, by choosing such terms, that the co-efficients in each equation will be multiples of 10, 100, 1000, etc.

If it is desired to set on the machine all the orders at the same time, it is necessary to make a further reduction of the quantities found from the equations. We prefer, however, to set them consecutively, after the computation has begun.

It is found, from our own work as well as that previously done with the machine, that it is occasionally liable to an accidental error, from the failure of one or more rings to perform its office. These errors are purely mechanical, and are not to be confounded with the principles on which the machine is constructed.

One of the first requisites is to hold the ring, on which numbers are engraved, so that there shall be no side play, and yet allow it to move with the necessary freedom. The second is, to be able to destroy the momentum of the ring, as soon as the motive force ceases to act. The latter condition has been obtained by putting a "brake" piece on each ring, consisting of a small piece of leather or rubber pressed against its circumference, by means of a spring. The liability of accidental error would be greatly lessened by connecting ratchet wheels with each ring, so that it could only move one direction. This would enable us to put more weight on the adding levers, without any danger of disturbing the position of the ring, when the motion of the shaft is reversed. A little attention to a few of these points would secure an almost perfect machine.

For bringing the type in line, previous to making the impression, we have employed a brass roller in place of the

steel wedge. This roller is pressed between the type by two rubber wheels, and is found to work admirably. The type are always straightened, no matter what their position may be, and without any possibility of injury to any part of the mechanism.

Our past experience has led us to believe that such a machine would be greatly enhanced in value, by the addition of one or two more orders of differences; since in that case, a much longer series of numbers could be computed from one set of constants.

It would be an easy matter to apply motive power to the machine, so that when once set, it shall be a complete automaton, making its computations without the assistance of any person. As soon as one set of constants are exhausted, the machine will stop, and will also be made to give notice of the fact by ringing a bell; upon which, a new set of constants may be introduced, and the computations continued.

---