Before exploring just what that idea was, it will
be necessary to explain in an elementary way another
aspect of the method of finite differences. First,
it will be remembered from Chapter Two that the fundamental
definition of finite differences is:
Again, it will be remembered that transcendental
functions (in this discussion the sine function will be
used as the example) do not have any order of difference
constant; that is, to tabulate a sine function precisely
would take an infinite number of columns in a difference
engine. In practice, this is not necessary, since the
higher order differences do become smaller; one can
substitute for the transcendental function an algebraic
function which approximates it over a given domain, then
manually alter the differences to proceed through another
domain, and so on. As the number of orders of difference
available becomes larger, the width of the domain that
can be tabulated without intervention increases also;
but as the number of significant figures to be retained
goes up, the possible domain shrinks. In practice, it
is possible to tabulate a sine function through a whole
quadrant only by breaking it up into many small domains.
To calculate a sine table at intervals of one minute with
eight significant digits, a machine which had a constant
fourth difference and fifteen digit capacity would have
to be reset about every two degrees
3

This approach Babbage found to be objectionable, for
two reasons. First, the necessity of manually altering
the setting of the machine several times in an operation
greatly increased the possibility of introducing errors
into the tables it produced, end this he wanted to avoid
at all costs; it also became more difficult to verify
the accuracy of a produced table, since it was no longer
true that if the first and last values were correct, the
whole table was correct. Second, Babbage found this
approach to transcendental functions to be theoretically
impure and inelegant; it did not satisfy his image of
the intimate relation that should be possible between the
machine and the mathematics on which it was based.
As it turned out, Babbage found that transcendental
functions could often be handled quite simply and elegantly
by a somewhat different approach to dealing with the fact
that they had no order of difference constant. This
can be seen in the following simple development.
Taking again the fundamental definition of the
method of finite differences, and assuming we want to
tabulate the function sin(x) from zero to ninety degrees
for increments of one degree, it follows immediately
that:
One's immediate impression is apt to be that this
relation is circular, since in order to generate new
values of the function by it, a difference engine would
have to predict those same values. But this is not in
fact the case. In order to generate sin(x+l) from sin(x),
one need know only a Δsin(x). Δ2sin(x) is needed only
to calculate sin(x+2), by way of calculating Δsin(x+l).
In fact, even though this difference equation applies
to the second difference of the function, no second
difference column is needed to use it. Instead, as soon
as sin(x+n) has-been calculated from Δsin(x+n-1) by
adding it to sin(x+n-1), we can simply add Ksin(x+n) to
Δsin(x+n-1) to form Δsin(x+n), from which sin(x+n+1)
follows, and so on.
But clearly, due to its theoretical priority and
its mechanical simplicity, a machine to calculate only
from equations of constant differences ought to be built
first. This was the course that Babbage adopted.
The first working model of the Difference Engine,
completed about the end of May, 1822, as well as the
full scale version whose construction was undertaken for
the government, were both of the simpler kind. However,
the section of the full scale machine which was put
together in 1832 had added on to it a special provision
for demonstrating the sort of technique by which
transcendental functions could be handled. It will
clarify Babbage's thinking in 1822 and after if we first
 consider this later device.
consider this later device.
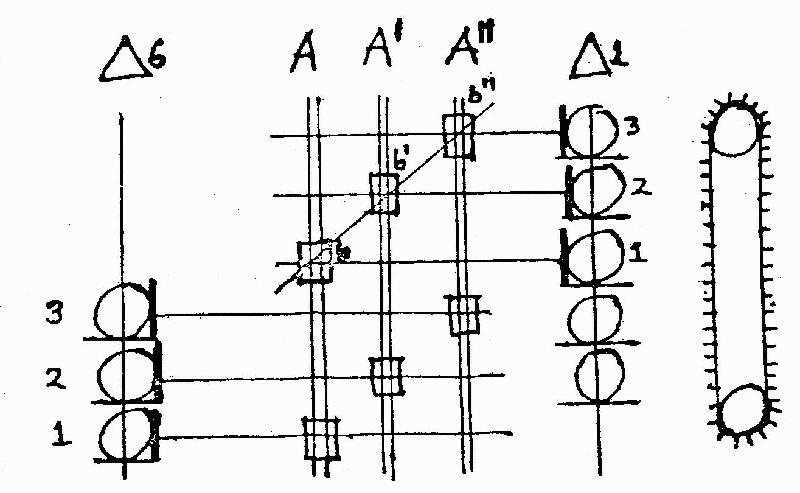
In the 1832 section, there were essentially three
vertical columns arranged parallel to one another across
the front of the machine to hold the table, first
difference and second difference. What Babbage did was
to add extra axes in front of the table column and the
second difference column; each of these axes had a wheel
on it which could be set to engage with any one of the
wheels on the column to which it was adjacent; further,
the two special axes were also geared together in such a
way that they always rotated together. In this way, a
single digit of the tabulated result, say the units digit,
could be fed back onto the second difference column, and
from there be added on to the first difference columns
if the special digits in the table and second difference
column were initially set equal, they would remain
equal throughout the calculation, since the second
difference digit would be continuously reset to equal
the table digit.
Thus Babbage demonstrated in a primitive way the technique
for tabulating transcendental functions. However,
this device was of no practical use, for two reasons: it
could handle only a single digit from the table column,
and even so, it could not multiply it by a special constant
before adding it back in, as would be required in a useful
computation.
 Returning now to 1822, it has already been stated
that the machine of which Babbage made a first working
model was one for computing functions with a constant
second difference and very few digits.
4
It was clear to
Babbage from the first that by using the same general
design the machine could be extended to employ greater
numbers of differences and digits, but this did not
satisfy him. He expressed his dissatisfaction with the
limitations of constant differences most clearly in the
paper he read to the Astronomical Society on December 13,
1822, in the following terms:
Returning now to 1822, it has already been stated
that the machine of which Babbage made a first working
model was one for computing functions with a constant
second difference and very few digits.
4
It was clear to
Babbage from the first that by using the same general
design the machine could be extended to employ greater
numbers of differences and digits, but this did not
satisfy him. He expressed his dissatisfaction with the
limitations of constant differences most clearly in the
paper he read to the Astronomical Society on December 13,
1822, in the following terms:
The principle of generation of this table was that
the second difference for any terms was equal to the
units figure of the table value of the next succeeding
term, or:
As has been discussed in Chapter Two, Clement
suspended work on the Difference Engine in March, 1833.
From then until July, 1834, the drawings and parts of
the machine (with the exception of the section which had
 been assembled in 1832) sat in his workshop idle, with
Babbage essentially not having access to them. But on
July 15, 1834, the parts and drawings were delivered in
Babbage's custody. However, as we have seen, he was
reluctant to proceed with construction until some new
understanding was reached with the government on mutual
rights and responsibilities with respect to future work.
While Babbage waited for the Prime Minister, the machine
waited as well.
been assembled in 1832) sat in his workshop idle, with
Babbage essentially not having access to them. But on
July 15, 1834, the parts and drawings were delivered in
Babbage's custody. However, as we have seen, he was
reluctant to proceed with construction until some new
understanding was reached with the government on mutual
rights and responsibilities with respect to future work.
While Babbage waited for the Prime Minister, the machine
waited as well.
Though Babbage did not proceed with any direct work
on the Engine, and felt quite disgusted with the
circumstances surrounding the project, he had by no means
lost interest in the basic idea of the machine. He
therefore occupied himself, while waiting, with re-examining
the basic plans. In particular, he tried to design a
mechanism which would allow the machine to handle difference
equations of the sort discussed in the first section of
this chapter.
This first stage consisted of attempts to develop
the method used in the 1832 section for demonstrating the
transfer of single digits from the table column to the
second difference column. The first item to be found is
a group of obscure sketches entitled "Plan for adding from
one axis to another a number multiplied by 10n."
12
But
it is not at all clear from the sketches what Babbage had
in mind.
On the next page, under the title "Plan for multiplying
any numbers on any Δ axis and adding them to any other"
Is the following sketch:
13
During the succeeding days or weeks, Babbage sketched
several variations on methods of effecting this transfer
from one end of the machine to the other, the process
which he called "the engine eating its own tail," to
describe its recursive character.
14
By a series of steps
which are not recorded, Babbage was led, shortly before
September 18, to the very important step of arranging the
 columns in a circle around large central wheels.
15
columns in a circle around large central wheels.
15
In an account of this period written much later, in
November, 1869, Babbage said that he had come to adopt
an arrangement of horizontal racks connecting the axes,
but then realized that if the columns were circularly
arranged, the highest and lowest order columns could
communicate directly, since they would be adjacent, and
no racks would be needed. He then realized that the
advantages of the racks could be retained in the new
design if they were replaced by large geared wheels in the
center. This account of the development is plausible, but
doubtless also somewhat of a simplification.
16
Exactly what this new arrangement was is not clear
from the 1834 sketch mentioned above, and there was no
written description of it. Apparently the difference
columns, soon to be called adding axes, were put around
one side of the circle; they were divided vertically into
a certain number of "cages," corresponding to their
separate digits. Special pinions could engage their
wheels with the central wheels as desired; the central
wheels were simply very large gears rotating freely on
a central axis; there were in fact two central wheels per
cage. On the other side of the central wheels were the
 "multiplying pinions," used to step up numbers on the
central wheels, that is, to multiply them by powers of
ten by moving their digits up a certain number of cages.
A particular digit would be transferred from, say, the
lower central wheel in one cage to the higher central
wheel in another cage higher or lower by a number corresponding
to the power of ten by which it was being multiplied; the
number of cages stepped would be determined by the way in
which the connecting gears on the multiplying pinions were
set. The multiplied number could then be taken off by a
desired adding axis from the higher central wheels.
17
"multiplying pinions," used to step up numbers on the
central wheels, that is, to multiply them by powers of
ten by moving their digits up a certain number of cages.
A particular digit would be transferred from, say, the
lower central wheel in one cage to the higher central
wheel in another cage higher or lower by a number corresponding
to the power of ten by which it was being multiplied; the
number of cages stepped would be determined by the way in
which the connecting gears on the multiplying pinions were
set. The multiplied number could then be taken off by a
desired adding axis from the higher central wheels.
17
This arrangement formed what might be described as
the final stage of the Difference Engine design, for in
filling in the details and making it workable, Babbage
was led to realize that there were much greater possibilities
lurking in the plan, ones which eventually led him to the
fully elaborated plan of the Analytical Engine.
What may be called the second stage of the
transformation from the Difference Engine to the Analytical
Engine began at this point, and continued until the summer
of 1836, by which time all the main principles had been
laid down, although many details remained to be filled in.
 The course of development during this period was so
complex that only the main outlines can be given here.
Further, it will be much easier to understand some
aspects of the design when they are explained in the context
of the operation of the machine as a whole, so such
explanations will be at times postponed.
18
The course of development during this period was so
complex that only the main outlines can be given here.
Further, it will be much easier to understand some
aspects of the design when they are explained in the context
of the operation of the machine as a whole, so such
explanations will be at times postponed.
18
The first subject to which Babbage turned was a
method for multiplication and division. Working on
multiplication was no real departure from the previous
phase, for it was necessary in order to use the kind of
recursive difference equations in which Babbage was
interested. But the fact that the multiplication pinions
could step numbers down as well as up, and the fact that
division was the inverse of multiplication, led Babbage
to try to make the machine capable of both.
Given the ability to step numbers up, multiplication
was fairly simple; the problem was to decide how many
times at each level of stepping the multiplicand should
be added to a result column. The method first devised was
as follows. The multiplier was on one adding column, say
 A1; the multiplicand was on A2; and the product was
to be produced on A3. Attached to each figure wheel on
the adding columns was a snail; this was a notched
spiral wheel with the steps on it corresponding to the ten
digits. When an arm from another column fell on this
snail, it could sense the digit at which the figure
wheel was set. In multiplication, an arm would first
sense the lowest cage on A1, and would set a special
wheel to the same digit; then this wheel would be
gradually "reduced to zero" by another wheel with a single
tooth, which would "gather up" the units of the selected
digit, one per revolution. With each revolution of the
gathering up wheel, all the digits on A2 would be added
to the central wheels; the cages of A3 being connected
in the same way to the central wheels, the multiplier
would be successively added onto A3. When the special
wheel was reduced to zero (i.e. when the multiplicand had
been multiplied by the first digit of the multiplier)
the following would happen. The snail opposite the second
cage of A1 would set the special wheel to equal the second
digit of the multiplier; also the multiplying pinions
would be set so that as the digits from A2 were put onto
the central wheels, they would be stepped up one cage
before being added to A3. The multiplicand would then
be multiplied by the second digit of the multiplier by the
same gathering up process, the snails and multiplying
pinions would be reset for another cage, and so on, until
A1; the multiplicand was on A2; and the product was
to be produced on A3. Attached to each figure wheel on
the adding columns was a snail; this was a notched
spiral wheel with the steps on it corresponding to the ten
digits. When an arm from another column fell on this
snail, it could sense the digit at which the figure
wheel was set. In multiplication, an arm would first
sense the lowest cage on A1, and would set a special
wheel to the same digit; then this wheel would be
gradually "reduced to zero" by another wheel with a single
tooth, which would "gather up" the units of the selected
digit, one per revolution. With each revolution of the
gathering up wheel, all the digits on A2 would be added
to the central wheels; the cages of A3 being connected
in the same way to the central wheels, the multiplier
would be successively added onto A3. When the special
wheel was reduced to zero (i.e. when the multiplicand had
been multiplied by the first digit of the multiplier)
the following would happen. The snail opposite the second
cage of A1 would set the special wheel to equal the second
digit of the multiplier; also the multiplying pinions
would be set so that as the digits from A2 were put onto
the central wheels, they would be stepped up one cage
before being added to A3. The multiplicand would then
be multiplied by the second digit of the multiplier by the
same gathering up process, the snails and multiplying
pinions would be reset for another cage, and so on, until
 the digits of the multiplier were exhausted.
19
the digits of the multiplier were exhausted.
19
No irony was intended above in saying that multiplication
was simple; compared to division it was. Thus even with
a one digit divisor, that digit had to be compared with
the first digit of the dividend (requiring two sets of
snails and feeler arms and other apparatus); if the latter
was equal or larger, the former was subtracted from it, and
the fact of subtraction was entered as a unit at the top
of the result column; then the comparison was repeated,
and so on. If the divisor digit was larger, then apparatus
had to be shifted to compare it with the next cage, and
the successive subtractions had to be registered on a
different cage, and so on. Dividing by a multi-digit
number was far more complicated, for if the initial
comparison of the top two digits of the divisor and dividend
showed that they were equal, the second digit of each had
to be compared to the other, and perhaps even the third
and subsequent ones, before the machine would know which
of the two numbers was larger.
At this point, Babbage's new machine was fearsomely
complex, even though its powers were still very limited,
and so far only the outlines of the parts needed had
been considered. Further, it would have been incredibly
 slow, for the time required for multiplication and division
would have been considerably longer than the sum of all
the digits in the multiplier or divisor times the basic
addition time. But Babbage considered that this simply
meant that he had to shorten the basic cycle time and
make the complex processes more efficient.
slow, for the time required for multiplication and division
would have been considerably longer than the sum of all
the digits in the multiplier or divisor times the basic
addition time. But Babbage considered that this simply
meant that he had to shorten the basic cycle time and
make the complex processes more efficient.
To shorten the cycle time, the fundamental operations
had to be improved; these were: basic addition, that
is, transferring digits from one wheel to another, and
carriage of tens between the wheels in a given column. In
the Difference Engine, addition had been made by bolting
the two wheels so that they would gear together, then
giving the first wheel a full revolution, unbolting the
second wheel from it after the proper number of digits
had been passed. In the Analytical Engine, Babbage thought
through a number of other possibilities. One involved
direct gearing between the two wheels, having a projection
in one be pushed up by an inclined plane after the proper
part of the revolution had been passed so that they were
lifted out of gear.
20
Another method was to have snails
and feelers to set extra wheels equal to the figure
wheels, and then add onto the receiving wheels by a
 gathering up wheel as in multiplication, but this took
more time.
21
gathering up wheel as in multiplication, but this took
more time.
21
The method ultimately adopted was taken from the
approach used as early as the beginning of October, 1834,
22
for the purpose of clearing a number off a column, or as
Babbage called it, reducing it to zero. This worked by
having the wheels turn freely on an axis which could be
moved up and down relative to them by a small amount;
fixed to this axis was a series of projecting arms, one
for each cage; on each figure wheel was a stud which
would be contacted by the projecting arm when the axis
was in its lower position. The number on the column
would be reduced to zero when it was disconnected from
the rest of the machine and the axis was lowered and
rotated through a full turn so that it pushed the studs
and thus the wheels around until they all were set to
zero. It was only some months later, apparently in
January, 1835,
23
that Babbage realized that the same
technique could be used for transferring numbers from one
wheel or column to another (and thus also for addition)
if they were simply left connected while the reduction
to zero was performed. Naturally this entered the number
on the second wheel in an opposite sense of rotation, but
 since most connections were made through a series of
wheels and pinions which could be made odd or even in
number at will,
24
this did not matter.
since most connections were made through a series of
wheels and pinions which could be made odd or even in
number at will,
24
this did not matter.
The second area of basic operation which required
improve went was the carriage mechanism. In the Difference
Engine, the carriage had been delayed and sequential; that
is, carriage could not be performed as a wheel passed from
nine to zero in addition, since this would interfere with
the separate addition proceeding simultaneously on the next
higher digit; therefore carriage was delayed until
addition was complete. Further, in performing a series
of carriages onto a column of numbers, it is quite possible
that a unit will be carried onto a wheel already standing
at nine, thus making necessary a second order carriage,
and so on; this problem is solved if the carriages are
performed sequentially, that is, first on the lowest
wheel, then on the next, and so on. This solution gives
rise to its own problem, however, since if a large number
of digits are used (and Babbage had in mind thirty or
forty for the new machine from quite early on) sequential
carriage can take a great deal of time, even considerably
more than the basic addition itself.
The first approach Babbage used to speed up carriage
was what he called hoarding carriage.
25
In this method,
 carriage was delayed not until a single addition was
complete, but until a series of nine additions had been
made. In the mean time, the carriages required by each
addition had been stored on a special set of wheels; when
carriage was to be made the numbers on these wheels were
transferred to the result wheels as in an ordinary
addition. This technique had two disadvantages, however;
these carriages could still require second order carriages,
so they would require either an additional mechanism to
take care of these, or else to be added separately for each
digit; both approaches would require extra time and
mechanism. Further, hoarding carriage would be effective
only in those cases where a whole string of numbers were
being summed together; if the machine were performing
isolated or separate additions, it would be no improvement
over the old method of carriage.
carriage was delayed not until a single addition was
complete, but until a series of nine additions had been
made. In the mean time, the carriages required by each
addition had been stored on a special set of wheels; when
carriage was to be made the numbers on these wheels were
transferred to the result wheels as in an ordinary
addition. This technique had two disadvantages, however;
these carriages could still require second order carriages,
so they would require either an additional mechanism to
take care of these, or else to be added separately for each
digit; both approaches would require extra time and
mechanism. Further, hoarding carriage would be effective
only in those cases where a whole string of numbers were
being summed together; if the machine were performing
isolated or separate additions, it would be no improvement
over the old method of carriage.
The second new approach Babbage tried, and the one he
eventually adopted (although perfecting it to his satisfaction
took more time than any other part of the machine),
was what he called anticipating carriage, since it allowed
the machine to anticipate that a second order carriage
would arise from a first order carriage, and perform then
at the same time. This operated by having a special
mechanism brought into play when the wheel onto which a
first order carry was being made already stood at nine;
then the special mechanism would cause a carry to be made
 onto the next higher wheel at the same time, and so on.
Thus all carrys could be performed in one step immediately
after addition in a time independent of the number of
digits in the column. The details of the many different
ways Babbage tried to accomplish this need not be considered
here, but the first attempts seem to have been made about
the end of October, 1834.
26
onto the next higher wheel at the same time, and so on.
Thus all carrys could be performed in one step immediately
after addition in a time independent of the number of
digits in the column. The details of the many different
ways Babbage tried to accomplish this need not be considered
here, but the first attempts seem to have been made about
the end of October, 1834.
26
Although it was clear to Babbage that anticipating
carriage would save a large amount of time, it was equally
clear that whatever the details of the version finally
worked out, the mechanism for carriage would be immensely
complicated in relation to that required for addition by
itself. This apparent drawback led Babbage to an important
step, namely that of separating the carriage mechanism from
the columns on which it was intended to act. Thus given
one or two carriage mechanisms which could be connected
at will with the central wheels or with any adding column
in use, a large amount of mechanism could be saved.
This was a most important step in the evolution of
the Analytical Engine, for as the same approach was
applied to other aspects of the engine, there gradually
emerged the notion of a central processing section in
which the various arithmetical functions were to be
carried out, distinct from the area where the numbers were
stored when not being manipulated. The central processing
 unit Babbage later came to call the "Mill," and the other
number columns he called collectively the "Store," this
fundamental distinction of course still exists in current
computers.
unit Babbage later came to call the "Mill," and the other
number columns he called collectively the "Store," this
fundamental distinction of course still exists in current
computers.
It is not clear exactly when Babbage devised this way
of organizing the machine, along with the specialization
of the carriage mechanism from which it flowed, but
apparently they developed gradually between November, 1834
and the early spring of 1835. During this time Babbage
continued to develop the process of division, with respect
to which he made a very important breakthrough in principle,
though again the exact dates of the different steps are
not clear. We can, however, say that the following had
been thought through by early in March, 1835.
27
The problem with division was still that of deciding
whether the divisor was smaller than the remainder at
any given point in the operation, so that subtraction should
occur. Babbage's first approach, that of comparing as
many digits as necessary by using snails (discussed
above), required too complicated a mechanism. His next
approach was to eliminate most of this mechanism by having
the machine assume that the divisor was larger than the
remainder if the two numbers had the same first digit;
thus the divisor would be stepped down a cage and also the
 successive subtractions would be registered on a lower cage,
and subtraction would proceed. The difficulty with this
approach was that on those occasions when the first
digits of divisor and remainder were equal but yet the
remainder was larger, the machine would perform ten
subtractions where it could have performed one, although
it would still produce the right answer; thus this method
was too time consuming.
successive subtractions would be registered on a lower cage,
and subtraction would proceed. The difficulty with this
approach was that on those occasions when the first
digits of divisor and remainder were equal but yet the
remainder was larger, the machine would perform ten
subtractions where it could have performed one, although
it would still produce the right answer; thus this method
was too time consuming.
The neat approach Babbage used was most ingenious.
The numbers on the divisor and remainder axes were copied
onto two subsidiary axes, and the first was subtracted
from the second; if the result was negative, that is,
if the highest wheel changed from zero to nine and tried
to carry down from the (non-existent) wheel above it,
then the divisor (back on its regular axis) had to be
stepped down a cage; if the result was positive; that is
if the top wheel did not change, then the subtraction could
proceed back on the main axes without stepping. Thus
all the snails and feelers and comparisons of digit to
digit were eliminated.
The final step was to reverse the roles of operation
and test in this last method. That is, the machine was
to assume that the remainder was larger than the divisor
and proceed with subtraction; if this assumption were
false, it would show up in that the remainder would turn
negative in the way indicated above; this would put the
machine into a special sequence where it would add the
divisor back to the remainder, subtract one from the
 quotient, and then step down the divisor and the cage in
which digits were registered in the quotient before again
making a subtraction. This improvement saved time, since
in general the total number of subtractions that had to
be made was considerably larger than the number of
steppings that had to be made.
quotient, and then step down the divisor and the cage in
which digits were registered in the quotient before again
making a subtraction. This improvement saved time, since
in general the total number of subtractions that had to
be made was considerably larger than the number of
steppings that had to be made.
Again, Babbage had been led for practical reasons to
a change in the machine which was to be of far reaching
importance; as the Analytical Engine evolved from this
point, Babbage applied this method of controlling divisions
to other internal decisions the machine had to make, and
eventually to general program branching itself.
By early 1835, the number of different kinds of
axes which had to be interconnected in different ways
depending upon what operation was to be performed had
grown so much that a new approach to controlling the
machine was required.
28
The basic technique was to have
connections between different axes made through a series
of pinions and possibly the central wheels; the axes
on which the pinions were held could be moved up and down
a small amount, and the particular position they were in
determined what connections were made. The problem of
control was thus the problem of governing the position of
 the pinions. This was to be done by what Babbage called
"traveling platforms," which moved up and down repeatedly
in the basic cycle of the machine; when a pinion axis
was to be raised, it was temporarily locked to a traveling
platform; when this reached the proper height, the axis
was unlocked from it and locked to some stationary support,
so that it would stay in the proper position.
the pinions. This was to be done by what Babbage called
"traveling platforms," which moved up and down repeatedly
in the basic cycle of the machine; when a pinion axis
was to be raised, it was temporarily locked to a traveling
platform; when this reached the proper height, the axis
was unlocked from it and locked to some stationary support,
so that it would stay in the proper position.
The connections between the pinion axes and the
traveling platforms were controlled by the barrels. These
were cylinders embedded with many studs arranged in rows;
the studs in a particular row would activate levers which
made the connections necessary for a particular step.
29
Successive steps would be controlled by successive rows of
studs, the active row being determined by rotating the
barrel.
In March and April, 1835, Babbage developed two
important improvements in the processes of multiplication
and division. First, on March 22, Babbage realized that
he could adapt the machine for double precision
operation.
32
In particular, Babbage realized that if he
made it possible for the top of one column to carry and
step to and from the bottom of another column, then he
could take two numbers of, say, forty digits each (the
number of digits he seemed to be planning on at this time),
and multiply them together, retaining eighty digits in the
product; then when this product was divided by a forty
digit divisor, the quotient would still have forty
significant digits. On the other hand, it would also
be possible to convert the machine generally; thus a
machine with sixty variables of twenty digits each could
be made into a machine of thirty variables with forty
digits each with no real mechanical change.
33

The second change in the way multiplication was to
be done was devised on March 30, and was called multiplication
by table.
34
In this scheme, the machine would start a
multiplication by forming a table of the multiplicand
multiplied by each of the digits from one to nine: this
would be placed on nine special axes, and could be formed
quite easily by simple addition. Then a snail wheel would
sense the first figure of the multiplier, and supply
it to a selecting mechanism, which would cause the
corresponding multiple in the table to be added to the
result axis. Then the result and the multiplier would
each be stepped up one place, and the operation would be
repeated for the second digit of the multiplier, and so on.
In this way, every digit of the multiplier could be taken
care of in one step, rather than requiring a number of
additions equal to the digit's value. Division could be
handled in a similar manner, although the problem of
selecting which particular multiple ought to be subtracted
from the dividend was considerably more complex. Babbage
did not develop the details of division by table as early
as those of multiplication.
It is interesting to note that it was at about this
same time that Babbage made the first public statement
of his invention of the new machine; this was in the form
 of a letter to the great Belgian statistician L.A.J.
Quetelet, who read it to the meeting of the Royal
Academy of Sciences at Brussels on May 7-8, 1835.
35
Without going into details of the machine or its capabilities,
Babbage said "I am myself astonished at the power I
have been enabled to give this machine; a year ago I
should not have believed this result possible." Babbage
also announced, with characteristic optimism, "that
the greatest difficulties of the invention have already
been surmounted, and that the plans will be finished in a
few months."
of a letter to the great Belgian statistician L.A.J.
Quetelet, who read it to the meeting of the Royal
Academy of Sciences at Brussels on May 7-8, 1835.
35
Without going into details of the machine or its capabilities,
Babbage said "I am myself astonished at the power I
have been enabled to give this machine; a year ago I
should not have believed this result possible." Babbage
also announced, with characteristic optimism, "that
the greatest difficulties of the invention have already
been surmounted, and that the plans will be finished in a
few months."
During these next few months and many more, Babbage
did indeed continue developing the machine, and he turned
his attention increasingly to less critical parts of the
Engine, ones which will not be discussed here in any
detail. For example, in the late spring of 1835, Babbage
began to reconsider his original basic plan of a circular
arrangement of the machines he sketched possible
arrangements using straight racks, and also combinations of racks
and central wheels.
36
He also devoted some attention
to the forms of output for the new machines as early as
July, 1835, he made some notes about a "curve drawing
 apparatus" which would turn numerical output from the
engine into graphic form.
37
In December, 1835, Babbage
was making plans for having the printing mechanism
completely separate from the rest of the engine, perhaps
in another room, with only one rack to convey the data
to it,
38
he also wished to be able to turn out single
copies of results by having the type print through carbon
paper, rather than making an impression in a stereotype
mold.
39
apparatus" which would turn numerical output from the
engine into graphic form.
37
In December, 1835, Babbage
was making plans for having the printing mechanism
completely separate from the rest of the engine, perhaps
in another room, with only one rack to convey the data
to it,
38
he also wished to be able to turn out single
copies of results by having the type print through carbon
paper, rather than making an impression in a stereotype
mold.
39
What must be realized at this point, though, is that
while the engine as a whole was becoming more and more
complex in some respects, some of its individual parts
were getting much simpler, due to the specialization that
had been made necessary by the very complexity introduced
into the particular processes. Most especially, the
separation of the Store from the Mill had made it possible
for the Store axes which held individual variables to be
very simple indeed, much simpler, for example, than one
of the columns in the Difference Engine. This of course
made it possible and practicable to have the machine able
to handle a very large number of variables; Babbage at one
time considered as many as one thousand.
40

But although Babbage could imagine problems which
would take advantage of this large capacity and also of
the rapidity and sophistication of processing of which
the Mill was now capable, the machine would not have been
able to solve these problems, because the control
mechanism was not able to handle the necessary instructions;
the process of placing studs for the different operations
in the drums by hand was far too limited, too cumbersome
and too inflexible to take advantage of the rest of the
engine.
This led Babbage, on June 30, 1836, to adopt punched
cards for the control of the engine.
41
These he adopted
quite directly from the system of control of automatic
looms by punched cards which had been perfected at the
beginning of the century by J.M. Jacquard of Lyons.
42
In
principle, these cards were identical to the Hollerith
punched cards used in twentieth century computers, in
that they consisted of cardboard rectangles with rows
and columns of spaces which could be punched out or left
solid, conveying information through some kind of sensing
mechanism to the machine which they were to control. In
practice, Babbage's cards were to be sensed by mechanical
 levers rather than by electrical brushes, so that they
had to be made of thicker cardboard, and their area was
also to be larger.
levers rather than by electrical brushes, so that they
had to be made of thicker cardboard, and their area was
also to be larger.
The introduction of punched cards into the new engine
was important not only as a more convenient form of control
than the drums, or because programs could now be of
unlimited extent, and could be stored and repeated without
the danger of introducing errors in setting the machine by
hand; it was important also because it served to
crystalize Babbage's feeling that he had invented
something really new, something much more than a
sophisticated calculating machine. The first indication
of Babbage's vision came in a memorandum in his notebook
dated July 10, 1836, sayings "This day I had for the
first time a general but very indistinct conception of
the possibility of making an engine work out algebraic
developments, I mean without any reference to the value
of the letters" (that is, the value of the letters in the
formulae with which the machine was dealing).
43
Unfortunately, the rest of this note is very obscure and
sheds no light on what Babbage had in mind, but from some
of the notes in the vicinity of the above quotation it
appears that one of the things Babbage had in mind was
eliminating between variables in high order simultaneous
equations.

In any case, by this time, midsummer of 1836, all
the main principles of the Analytical Engine had been laid
down; if one were obliged to name a single point at which
it was "invented," this would be it. From this point
on, Babbage's task was essentially to fill in the details,
although this phrase cannot do justice to the magnitude
of what he did. The character and complexity of those
details, and indeed what it was that Babbage had by this
time invented, can only be understood in terms of the
general structure and operation of the machine as a whole.
No description of the mechanical operation of the
Analytical Engine has ever been published, and it is
doubtful that anyone other than Babbage has ever understood
it fully, and very few have understood it at all.
Fortunately, in December, 1837 Babbage wrote a paper
"On the Mathematical Powers of the Calculating Engine,"
of fifty three manuscript pages, which provides a rather
full, if sometimes less than lucid, account of the operation
of the machine.
44
The following description of the Analytical Engine
is drawn largely from this 1837 paper, being quoted directly
 when appropriate, although the original material has been
rearranged and condensed, with some explanations rewritten
or added as necessary.
45
.
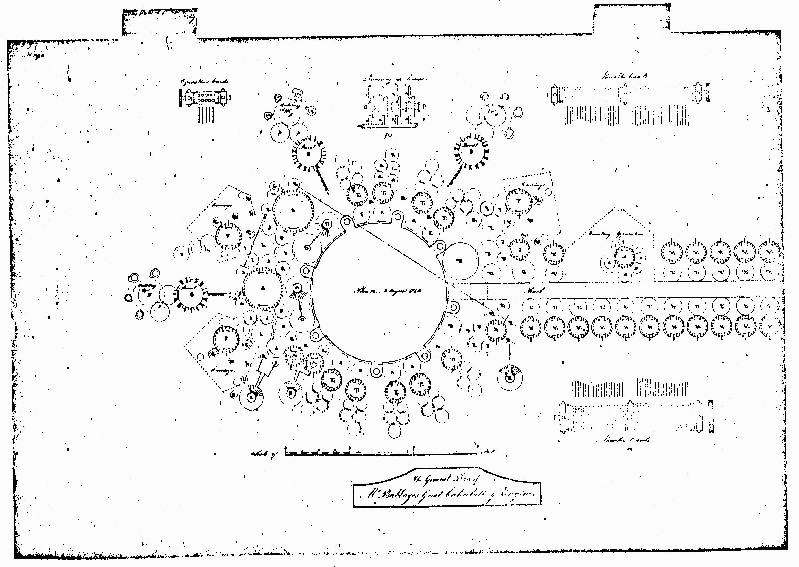
The Analytical Engine consisted of two sections,
the Store and the Mill. Figure 1 is a plan of the Engine
drawn in August, 1840, but basically the same as what
Babbage described in 1837. The Mill was the collection
of circles and devices surrounding the large central
wheels in the middle of the drawing. The Store was the
section extending off toward the right from the Mill;
not all of it is shown. It can be seen from the scale
provided. in the drawing that the length of the part of
the Engine shown was about ten feet.
when appropriate, although the original material has been
rearranged and condensed, with some explanations rewritten
or added as necessary.
45
.
The Analytical Engine consisted of two sections,
the Store and the Mill. Figure 1 is a plan of the Engine
drawn in August, 1840, but basically the same as what
Babbage described in 1837. The Mill was the collection
of circles and devices surrounding the large central
wheels in the middle of the drawing. The Store was the
section extending off toward the right from the Mill;
not all of it is shown. It can be seen from the scale
provided. in the drawing that the length of the part of
the Engine shown was about ten feet.
Running down the middle of the Store was a series of
long racks, one for each cage; any column in the Store
could be engaged with these racks. At their left end, the
racks connected with the central wheels of the Mill. The
section of the Store beyond the edge of the drawing was
simply a continuation of the part shown.
At the beginning of a computation, the numerical data
could be fed into the Store by manually setting each wheel
of the columns being used. However, it was also possible,
and obviously preferable, to feed the data in by a special
set of punched cards, called the "Number Cards." These
cards had another function which Babbage considered even
more important. It might happen that in some very complex
computation, more variables would be needed than there were
columns in the Store; in this case the Store could be
 directed to punch certain cards to hold the overflow
data, which could later be recalled and read back into
the machine as needed.
48
directed to punch certain cards to hold the overflow
data, which could later be recalled and read back into
the machine as needed.
48
The Store also contained various output provisions.
Single copies could be printed through carbon paper;
copper plates were punched when the results were to be
published. Most interesting was the Curve Drawing
Apparatus:
However, Babbage considered that it would probably
be best to have all output from the Store in the form of
punched cards. These would then be fed into a totally
separate (off-line) printing mechanism which would produce
whatever form of output was desired.
The functioning of the Store was controlled by a set
of Variable Cards, whose action was co-ordinated with the
Operation Cards which controlled the Mill. The Variable
 Cards could order a number to be given off from a
particular store axis to the ingress axis of the Mill,
or for a number to be received from the Mill and put on a
particular store axis; the Variable Cards also could order
that numbers be read and stored from the Number Cards, or
that particular variables be punched on cards.
50
Cards could order a number to be given off from a
particular store axis to the ingress axis of the Mill,
or for a number to be received from the Mill and put on a
particular store axis; the Variable Cards also could order
that numbers be read and stored from the Number Cards, or
that particular variables be punched on cards.
50
The actual operations were performed in the Mill. It
was made up of the following principal components: Figure
Axes, Carriage Axes, Table Axes, Digit Counting Apparatus,
Selecting Apparatus, Barrels, Reducing Apparatus, Operation
Cards, and Combinatorial Cards. These components were
described by Babbage as follows (and see Figure 1).
1. Of the Figure Axes
The Figure Axes A and 'A are connected with
each other without the intervention of the central
wheels so that a number on the figure wheels of one
axis may be transferred to those of the other.
These figure wheels are considerably larger
than any others in order to allow of sufficient space
on their circumference for placing the pinions by
which communications are made with other parts of
the mill.
By means of some of these pinions a process
called Stepping down and another called Stepping up
may be performed. It consists in shifting each digit
of a number one cage lower or one cage higher, which
processes are equivalent to the arithmetical operations
of dividing or multiplying the number by ten.
Other pinions are fixed on register axes R
and Ri and convey the two highest figures of the
dividend to the Selecting apparatus.

The third figure axis, ''A, is placed near the
Store and constitutes the egress axis. It is
adjacent to the digit counting apparatus, with
which it communicates.
2. Carriage Axes.
These Axes F, 'F, ''F with their peculiar apparatus
are employed to execute the carriage of the tens
when numbers are added to or subtracted from each
other. The carriages F and 'F can be both connected
with the Figure axis A, or one of them with the
Figure axis A and the other with 'A, or they may by
means of the central wheels be connected with any
other part of the Mill. The third carriage, ''F,
is connected with both the Mill and the store and may
be used with either.
Whenever. the number subtracted is greater than
that from which it is taken the resulting carriages
would, if effected, and if the mechanism admitted,
produce a carriage in the forty first cage. This
fact is taken advantage of for many purposes: it
is one of very great importance and when it happens
a Running up, is said to occur. Connected with this
part is a lever on which the running up warning acts,
and this lever governs many parts of the engine
according as the circumstances demand.
3. Table Figure Axes.
These axes are ten in number; nine of them
contain the table of nine multiples of one
factor in Multiplication and of the Divisor in
Division. The tenth contains the complement of the
Divisor in the latter operation. They are all
connected with the central wheels and the number on
each figure wheel can be stepped up or down upon
the other figure wheel of the same cage. The figure
which at each stepping goes off from the bottom wheel
is transferred to the top wheel.
4. Of the Digit Counting Apparatus.
This is a mechanism by which the digits of any
number brought into the mill may be counted; and
certain calculations made as to the position of
the decimal point in the result of multiplication and
Division. It is also used to limit the number of
figures employed when the engine is making successive
 approximations either to the root of equations or to
the values of certain functions. It consists of
three distinct systems nearly similar to each other.
approximations either to the root of equations or to
the values of certain functions. It consists of
three distinct systems nearly similar to each other.
5. Of the Selecting Apparatus.
When a table of the nine multiples of a
multiplicand has been made it becomes necessary in
order to effect multiplication to select successively
those multiples indicated by the successive digits
of the multiplier.
This mechanically is not difficult. But when
in the process of division it becomes requisite to
select that multiple which is next less than the
divident from which it is to be subtracted, the
mechanical difficulty is of quite a different
order, and hitherto nothing but the most refined
artifices have been found for accomplishing it. . . .
[6.] Of the Barrels.
The barrels are upright cylinders divided
into about seventy rings, the circumference of each
ring being divided into about eighty parts. A stud
may be fixed on any one or more of these portions of
each ring. Thus each barrel presents about eighty
vertical columns every one of which contains a
different combination of fixed studs. These barrels
have two movements. 1st They can advance horizontally
by a parallel motion of their axis. 2nd They can
turn in either direction and to any extent on their
axis.
When the barrels advance horizontally these
studs act on levers which cause various movements
in the mill: the stud belonging to each ring giving
a different order.
Amongst these movements or rather these orders
for movements the following may be more particularly
noticed.
The advanced of a barrel may order:
- A number with its sign to be received into the
mill from the ingress axis;
- A number with its sign to be given off from the
mill. This number may thus be altogether obliterated
from the mill: or it may at the same time be
received on the egress wheels or the number may be
 given off from the mill to the egress wheel and
at the same time be itself retained in the mill.
given off from the mill to the egress wheel and
at the same time be itself retained in the mill.
- A variable card to be turned.
- An operation card to be turned.
- The circular movement of the Barrel itself or of
any other barrel to another vertical. This always
occurs at every step from the beginning to the end of
what are called operations. The barrels when once
ordered by the operation cards from their zero point
to any given vertical always direct themselves to be
turned to another vertical preparatory to their
next advance. This circular motion is however
occasionally changed by an action arising from
another source.
7. Of the Reducing Apparatus.
Behind each barrel is placed a reducing apparatus.
It consists of six or eight sectors which can
be made to act upon the barrel and give it a
rotatory movement so as to make it pass over 1, 2, 3,
or any required number of verticals previously to its
next advance. The levers which put these sectors
into action are acted upon by
- The studs on their own barrel..
- The studs on any other barrel.
- The Operation Cards.
- The Running up levers.
The first and third of these sources of action occur
most frequently.
51
8. Of the Operation Cards.
Those who are acquainted with the cards of a
Jacards [sic] loom will readily understand the
functions performed by these cards. To those who
are unacquainted with that beautiful contrivance it
may be necessary to state that the Cards consist of
pieces of thick paste board, tin plate, or sheet
zinc, pierced with a number of holes. These cards,
being strung together by wire or tape hinges, pass
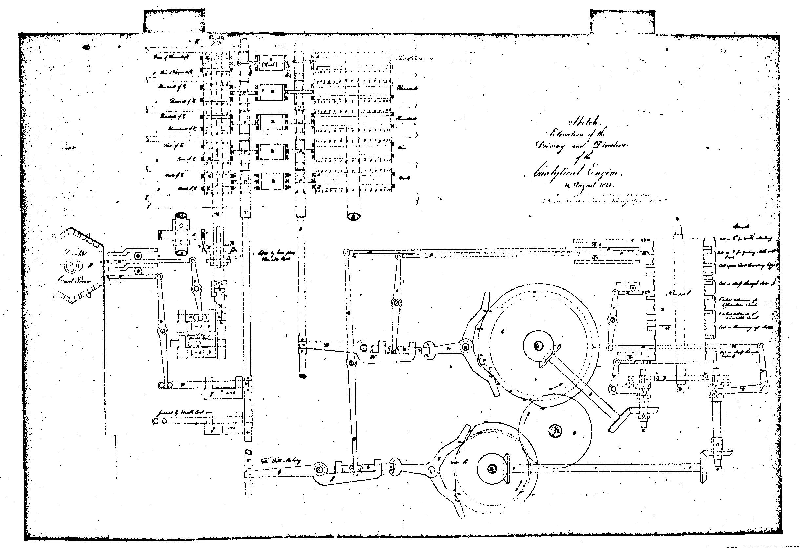
FIGURE 2: Driving and Directive of the Analytical Engine,
August 14, 1841. S.K., Drawing II, 94.
 over a square prism. The prism is situated
in front of a number of levers placed in rows which
govern the Reducing Apparatus and consequently the
barrels. The faces of the prism are perforated so
as to present an opening opposite every lever.
If the prism alone is made to advance
horizontally against these levers then the levers themselves
will enter into the holes of the prism and be partly
covered by it; but they will not be moved out of
their places.
over a square prism. The prism is situated
in front of a number of levers placed in rows which
govern the Reducing Apparatus and consequently the
barrels. The faces of the prism are perforated so
as to present an opening opposite every lever.
If the prism alone is made to advance
horizontally against these levers then the levers themselves
will enter into the holes of the prism and be partly
covered by it; but they will not be moved out of
their places.
Again if a card having as many holes as the
prism has, or as there are levers opposite to it, is
placed upon the advancing face of the prism, no
effect can be produced on the levers by this advance
of the prism. But if a card having one hole less than
the prism is placed on its face, then when the prism
advances the lever opposite that hole will be pushed
away and any order given for which that lever was
appointed.
Suppose after every order the levers to be
replaced, and let the prism be turned one quarter
round, then a new card will be presented to the
levers, and if one or more holes of this second card
are stopped up, a different order will be transmitted
through the levers to the Reducing Apparatus and
thence to the barrels.
Thus by arranging a string of cards with properly
prepared holes any series of orders however arbitrary
and however extensive may be given through the
intervention of these levers.
The number of the levers acted upon by the
operation card is small: they respectively direct
the barrels to commence the following operations:
- The Addition of two numbers.
- The Subtraction of one number from another.
- The Multiplication of two numbers.
- The same Multiplication limited to a given
number of the first figures.
- The Division of one number by another.
- The same Division limited to a given number
of figures in the quotient.
The levers numbered 4 and 6 are rarely used;
the extraction of roots being the only case in which
they are required.
These cards are called into action by orders
from the barrels. What they shall do when acting
 depends on the nature of each individual card. What
repetitions they shall be subject to depends on
the orders communicated to them from the Combinatorial
Cards and their Counting Apparatus. Many calculations
are much simplified by having two sets of Variable
Cards.
depends on the nature of each individual card. What
repetitions they shall be subject to depends on
the orders communicated to them from the Combinatorial
Cards and their Counting Apparatus. Many calculations
are much simplified by having two sets of Variable
Cards.
9. Of the Combinatorial Cards.
One or more peculiar cards may be inserted among
the operation cards of certain formulae. They are
called Combinatorial Cards.
The object of these cards is:
To govern the Repeating Apparatus of the Operation
and of the Variable Cards and thus to direct at
certain intervals the return of those Cards to given
places; and to direct the number and nature of the
repetitions which are to be made by those cards.
Whenever Combinatorial Cards are used other
cards called index cards must occur amongst those
of the formulae. The use of these cards is to
compute the numbers which are to serve successively
for the indices of the combinatorial cards. At
what time the Combinatorial Cards shall act depends
on the number of repetitions the last of those cards
appointed. What orders each Combinatorial Card shall
give depends on the nature of each individual Card.
52
Thus the detailed steps within an arithmetical operation
were controlled by the Barrels, while the sequence of
operations was determined by the operation cards. The
interaction between the two occurred as follows:
In any operation it is only necessary that the
operation card ordering its commencement should be
advanced. This sets the barrels in action and
provides through the variable cards if necessary the
first quantity to be operated upon; the barrels there
call in the other quantities required at the proper
times, until the operation is completed, the Mill
cleared of all numbers, and the computed result
 placed in its intended situation in the Store. The
last vertical on the barrels belonging to each
operation directs them to move to its zero point.
placed in its intended situation in the Store. The
last vertical on the barrels belonging to each
operation directs them to move to its zero point.
Such being the arrangement, the calculation
of numerical quantities resulting from two or more
successive operations may be readily performed by
placing the operation cards, strung together in their
proper order on their revolving prism, and the
variable cards marking the numbers in the Store on
[sic] which are to be the subjects of those operations
and also in the order in which they are required on
their own revolving prism, and then putting on the
final verticals of one of the barrels a stud which
orders the operation cards to advance.
53
The actual operation of addition as controlled by the
Barrels was performed by the method of reduction to zero
already discussed; that is, the Store axis off which a
number was to be read was connected to the Mill axis
which was to receive the number, and then the wheels of
the former were set mechanically to zero, transferring
the number to the Mill. Similarly, carriage was performed
by the method of anticipation already discussed, although
Babbage never finally settled on the details of the carriage
mechanism.
The only new or complex element in the process of
addition was the treatment of signs, since addition and
subtraction were to be performed alike, and since the
machine could now contain both positive and negative numbers
in the Store. This was to be done in the following way.
 Suppose two numbers were to be combined; each would have
two signs, one corresponding to addition and subtraction,
as specified by the operation cards (Babbage called this
the algebraic sign), the other corresponding to whether
the number actually in the Store as determined by previous
operations was positive or negative (called the accidental
sign). As a number came onto the ingress axis of the Mill
from the Store, the two signs would be compared, simply
by adding the pseudo-numbers on their topmost wheel, or
sign wheels as a positive sign corresponded to an even
number on this wheel, and a negative sign corresponded
to an odd number, the result of the addition of the two
digits would correctly indicate the combination of the
algebraic and accidental signs. If this combined sign was
positive, the number was added to the figure axis where
addition was to take place; if it was negative, the number
was subtracted, that is, an extra pinion was introduced
into the train of gears to reverse the direction of
rotation.
Suppose two numbers were to be combined; each would have
two signs, one corresponding to addition and subtraction,
as specified by the operation cards (Babbage called this
the algebraic sign), the other corresponding to whether
the number actually in the Store as determined by previous
operations was positive or negative (called the accidental
sign). As a number came onto the ingress axis of the Mill
from the Store, the two signs would be compared, simply
by adding the pseudo-numbers on their topmost wheel, or
sign wheels as a positive sign corresponded to an even
number on this wheel, and a negative sign corresponded
to an odd number, the result of the addition of the two
digits would correctly indicate the combination of the
algebraic and accidental signs. If this combined sign was
positive, the number was added to the figure axis where
addition was to take place; if it was negative, the number
was subtracted, that is, an extra pinion was introduced
into the train of gears to reverse the direction of
rotation.
The same process was applied to the second number as
it came into the Mill, and it would be added or subtracted
from the Figure Axis as determined by its combined
sign (and the same could be done with a third or subsequent
number in the same way). The effect of this addition or
subtraction might be to change the. sign of the number
on the Figure Axis by making it pass through zero; the
number on the Figure Axis would then appear as the complement
 of its arithmetic value; but the engine would know this
because a running up would have taken place, so that before
the result was used or returned to the Store it would
be changed back to its proper form, along with the finally
correct sign.
54
of its arithmetic value; but the engine would know this
because a running up would have taken place, so that before
the result was used or returned to the Store it would
be changed back to its proper form, along with the finally
correct sign.
54
Multiplication
The process of multiplication is thus performed
by the Engine:
The two factors P and Q with their respective
accidental signs being placed on the two sets of
Figure wheels No. 1 and No. 2 of the Ingress axis,
an operation card is turned. This directs the
barrels through the reducing apparatus to move
circularly to the vertical which commences multiplication.
At the next turn the barrels advance and order
the reception of one of the factors, Q. They also
direct themselves to move on their axes to the second
vertical belonging to multiplication. At the third turn
the barrels advance and order the reception of the
other factor, P, from the second set of Ingress wheels.
At this turn the factor P is subtracted from the
factor Q, which had at the preceding turn been placed
upon the figure wheels of 'F.
The result of this subtraction determines which
of the two factors is largest, and consequently which
factor is to be tabulated. Much time is saved by
this decision, for supposing one factor to contain
only four places of figures and the other to contain
thirty five figures, then if a table of the first
nine multiples of the first factor were made, its
multiplication by the other factor would require
thirty five additions, whilst if the larger factor
had been tabulated, only four additions would have
been necessary. The mechanical mode by which this
knowledge is conveyed to the barrels is thus.
The barrels, after ordering the subtraction of P
from Q in the axis 'F, direct themselves to move on to
 another vertical; if P is less than Q no Running up
takes place, and the order thus given by the barrels
is obeyed; but if P is larger than Q then a Running
up takes place, and the order given by the barrels to
move to a certain vertical is enlarged, and they
are directed by the running up lever to move on to
a different vertical. This new vertical directs
the tabulation of the second factor, whilst the
former vertical appointed that of the first factor..
another vertical; if P is less than Q no Running up
takes place, and the order thus given by the barrels
is obeyed; but if P is larger than Q then a Running
up takes place, and the order given by the barrels to
move to a certain vertical is enlarged, and they
are directed by the running up lever to move on to
a different vertical. This new vertical directs
the tabulation of the second factor, whilst the
former vertical appointed that of the first factor..
At the next turn the number which the Mill
has decided on tabulating is added to each of the
nine table axes and to the carriage F.
At the next turn the same number is added to
eight of the Table axes and the carriage axis, then to
seven, and so on, until the nine multiples have all
been formed on the nine Table axes.
During these turns the number of the digits in
the multiplier has been ascertained and placed in
the Counting Apparatus No. 1.
The Multiplier having been prepared is now
stepped down and acts upon the Selecting Apparatus.
Whatever digit exists in the lowest figure of the
multiplier, by means of the Selecting Apparatus the
corresponding Multiple is added over to the product
axis 'A. During this addition each multiple is
stepped up one cage higher on its own figure wheels;
also the multiplier being stepped down, its next
figure is conveyed to the Selecting Apparatus
preparatory to the next addition to the product.
The product is thus formed beginning with its
lowest figure on the figure wheels of the axis ['A];
but in the process of stepping up, the highest figure
on the tables axes may at length reach the top or
40th cage of their axes. At the next stepping the
highest figure would of course be stepped off the
machine and lost, but this is prevented by a communication
with the lowest figure wheel on the same axis to which
the number stepped off from the highest is transferred.
These figures which are so transferred to the lower
cages are not added to the same axis but are by a
particular mechanism added over to a set of figure
wheels on the axis A and the carriage F on which the
head of the product is formed.
If a number of twenty figures only is multiplied
by another factor containing an equal number of digits,
 as the product will not exceed forty digits it
will be contained on the first axis. But if both
factors contain forty digits then the head or first
forty digits of the product will be formed on
the axis A and the tail or second forty digits of
the product will be formed upon 'A.
as the product will not exceed forty digits it
will be contained on the first axis. But if both
factors contain forty digits then the head or first
forty digits of the product will be formed on
the axis A and the tail or second forty digits of
the product will be formed upon 'A.
The signs which entered with the original
factors, having been added together on the sign
wheels, will give the resulting sign of the
product. For if they were both positive, then each
sign being equivalent to an even number, the sum of
the two signs would give an even number or its
equivalent the positive sign. If on the other hand
both signs were negative, then a negative sign being
equivalent to an odd number, the sum of two odd
[numbers] produces an even number, which is also
equivalent to the positive sign which the product
ought in this case to possess. Lastly, if the sign
of one factor be positive and that of the other
negative, then the sum of an even and of an odd
number being odd, the negative sign results.
The termination of Multiplication arises from
the action of the Counting Apparatus, which at a
certain time directs the barrels to order the product
thus obtained to be stepped down so that the decimal
point may be in its proper place, and then to turn
to another vertical the consequence of which is the
transfer of the product with its proper sign to the
wheels on the egress axis from whence they may be
removed by Variable cards and the barrels to any
axis in the Store.
55
Division
Of the numerous difficulties which the
contrivance of an engine to perform arithmetical
operations presented, none certainly offered more
reasonable grounds of difficulty than that structure
of it by which it should be enabled to perform the
operation of division. . . .
It has already been stated that when any number
which happens to be greater than another is subtracted
from that other number, an event which has been termed
a Running up takes place, and that in consequence
 of this event any order which may be desired can be
given to any part of the engine. Bearing this fact
in mind, the division of one number by another
may be conceived to take place in the following
manner. . . .
of this event any order which may be desired can be
given to any part of the engine. Bearing this fact
in mind, the division of one number by another
may be conceived to take place in the following
manner. . . .
The first direction given by the barrels is to
subtract the divisor from the dividend. This order is
repeated until . . . it is found that a Running up
has taken place, a fact which of course indicates
that the divisor has been subtracted once too often.
The number of times the divisor has been subtracted
is marked by a register axis. Now it is in consequence
of this fact of a Running up that the engine knows it
has subtracted the divisor once too often, and that
knowledge is conveyed by the running up levers to the
barrels in the form of an order to move to such
verticals that at the succeeding turns they shall
direct the erroneous subtraction and registration
to be corrected, and the remainder of the dividers,
to be stepped up, in order to undergo a similar process
for the Discovery of the next digit in the quotient. . . .
The first figure in the quotient being thus
obtained, a repetition of the same process will of
course produce the succeeding figures.
The complete understanding of this principle is
of some importance, for it not merely relates to the
process of division, but it is capable of being
applied to any tentative arithmetical process. I
had applied it to the extraction of roots, but other
improvements induced me to dispense with it in this
instance. Its application is not limited to existing
rules, but I believe I may venture to state that
whenever new methods are contrived for overcoming
arithmetical difficulties by tentative processes,
it will be found available for these new purposes;
and that even in cases where the tentative processes
relate to algebraic expressions it may yet be useful.
I have given a simple case in order to explain
the nature of this principle. Division however is
not executed by this tedious process, which would
required for its performance a number of turns more
than equal to the sum of the digits in the quotient.
The process really used may be thus described.
The operation card ordering division having
advanced directs the barrels to the proper verticals.

The divisor P is first received from the ingress
wheel upon several parts of the mill.
The Dividend B next enters. Several processes
are gone through in order to ascertain whether it
will be necessary to step the dividend up or down,
and how many steppings there ought to be of either
kind. This depends upon the number of digits of the
quantities operated upon, and is principally executed
by the counting apparatus, which also computes.
the number of figures which must occur in the Quotient.
At about the eighth turn the formation of
the table commences, and also the selecting apparatus
is prepared.
If the Stepping down is completed, the actual
division may commence about the eighteenth [?] turn.
By means of the selecting apparatus the two
first figures of the dividend are compared with the
first two figures of each of the nine multiples of
the divisor, and that multiple which has its two
first figures either equal to or nearest less
than the first two figures of the dividend is
selected and subtracted from the dividend.
The remainder is then stepped up, and the
process repeated until the counting apparatus
interferes to finish the process.
In case the two first figures of the dividend
are exactly the same as the two first figures of one
of the multiples of the divisor, there may arise a
doubt whether that multiple or the proceeding one
should be subtracted: this will depend on the
third figure of each quantity. But in this case the
mill always takes for granted that the multiple
selected is the true one. If however the contrary
happens to be the case, then the subtraction of the
multiple which is really too large will cause a
running up in the dividend, and in consequence of
this, orders will be transmitted to the barrels
to direct the addition of the first multiple and the
subtraction of unity from the multiple registered in the
quotient, by which means, the quotient being set
right, the first process is then continued.
After the end of the actual division, the quotient
and the remainder, if required, are given off to the
egress wheels.

As the result of the multiplication of a number
containing forty digits by another of equal extent
is a product containing eighty digits, and as this
product can be conveyed into the store on two sets
of figure wheels, a provision has been made for
bringing such numbers back into the mill when they
are to become dividends, so that the results
of the division of a number eighty by one of forty
digits shall have the forty figures of its quotient
true to the last figure.
56
This completes the explanation of the outlines of
the four basic arithmetical operations. But it will be
well to provide, as Babbage did not, a brief account of
the mechanical approach of a lower level by which the
various connections referred to were controlled.
The fundamental notion necessary for understanding
this is one that Babbage called Chain. This can
be understood from the following sketch:
57

Here the power input is on the shaft N; this turns
a wheel holding the cams B and D, which act through a
rocker-arm to move the piece E back and forth. E slides
along a similar piece, called G; G and E will be connected
together if the link C is in position in the slot cut
away in them, and in this case the rotation of N will
cause G to oscillate. The position of C, which pivots
around the axis T, is controlled by the small arm F.
The principle involved is that the transmission of
power from N to G is controlled through a link which acts
rather like a switch, and can be operated with much less
power than it is controlling. Thus F might in fact be a
feeler which senses whether a hole is punched in a certain
position in a card.
The way the principle of Chain was applied in practice
in the Analytical Engine can be seen in two crucial cases
in Figure 2. In it, a variable card can be seen on the
left and a Barrel on the right, with the columns they
control near the top. One chain can be seen from the
large cam wheel, C, next to the Barrel; the rocker arm
H will rock the arm K, which will move the pinion axis
that can connect the Rack to the figure axis up or down;
but this chain will only be complete if the link B is
in the proper position, as determined through a couple of
arms by a stud near the top of the Barrel. Other arms
forming Chains from the Barrel to other axes or to effect
 the rotation of the Barrel itself are activated by
different studs, but only a few are shown in this drawing.
the rotation of the Barrel itself are activated by
different studs, but only a few are shown in this drawing.
The Variable Cards form Chains of a slightly different
kind. Again, their function is to raise a column with
pinions so that a certain Store axis will be connected
to the Store Rack. They act through what were called
Travelling Platforms, which were shafts below the main
machinery which move up and down a small amount at
regular intervals; they are shown to the right of the
variable cards in the drawing in cross-sections marked P.
Arms activated by the variable cards would connect or
disconnect the Travelling Platforms from the pinion axes
through special sliding links.
One final and slightly different example of a Chain
is the technique used for anticipating carriage. The
examples of Chains given above are ones where a power
train would be completed if one certain contingency were
fulfilled. In the Chain involved in anticipating carriage,
there were multiple contingencies of different kinds. Thus
the beginning of the chain would be moved if there:
was a first order carriage at a certain point in the
number column; the link would be activated if the wheel
next above stood at nine (in the case of addition);
the chain could be as long as the series of adjacent
wheels standing at nine, or there could be several,
separate partial chains set up in a column at the same
time.

One final aspect of the operation of the Analytical
Engine must be considered here, both because an understanding
of it is important in any assessment of the Engine, and
because Babbage himself considered it very important;
this is the question of the speed of the Engine.
In his 1837 paper, Babbage proposed several principles
which had guided the design of the machine, one of them
being "that the several operations shall be executed in
the shortest possible time."
58
Babbage described the great
difficulty this principle had caused him, and why he
considered it to be extremely important, in the following
remarks, which indeed, serve also to express in a way the
fundamental paradox of Babbage's project, and also some
of the motivation which drove him on.
In fact the whole history of the invention
has been a struggle against time. As soon as any
contrivance has been made which was unexceptionable
as to the mechanism, the question has always arisen:
Can it not be executed in less time by some other
contrivance? Thus every advance has but raised up
a new object of rivalry, itself to be superceded
by some more rapid means; nor can I hope that I
have nearly reached the limit. If I have approached
it, it is more than I have a right to expect as the
pioneer in this difficult career. Another age must
be the judge of that as well as of the other
questions relating to the Engine. . . .
The reader who only looks at the mechanical
difficulties in contriving such an engine will
doubtless be surprised, when he examines the history
of the contrivances, . . .. at the lavish rejection of
 inventions which has taken place in order to achieve
rapidity in execution. But the Analyst, who is
aware that the last resource in all our difficulties
is the conversion of the most intractible expressions
into infinite series, will more readily appreciate
the importance of even a small abbreviation of the
time, when he is informed that it is one of the
objects of this engine to arrive at the numerical
values of the coefficients of such series, however
complicated the laws by which they are formed;
and proceding again from these results as established
data, it is proposed to assign the values of such
expressions for any magnitudes of the variables.
59
inventions which has taken place in order to achieve
rapidity in execution. But the Analyst, who is
aware that the last resource in all our difficulties
is the conversion of the most intractible expressions
into infinite series, will more readily appreciate
the importance of even a small abbreviation of the
time, when he is informed that it is one of the
objects of this engine to arrive at the numerical
values of the coefficients of such series, however
complicated the laws by which they are formed;
and proceding again from these results as established
data, it is proposed to assign the values of such
expressions for any magnitudes of the variables.
59
As to the actual time taken, Babbage first defined
the unit of time in which to describe the length of
operations as that required for a figure wheel to pass
over one unit of number, as to go from zero to one. Then
the minimum cycle for adding one number would be ten units,
nine for units which might be added, and one for another
digit which might be carried; this cycle of ten, he
thought, was the theoretical minimum which any decimal
machine could ever attain. In practice, the cycle had
to be longer, for time had to be allowed for moving the
connecting pinions into place and for making the lockings
and unlockings which prevented the machine from making
any mistakes; the extra time required brought the cycle
up to fifteen units in the case of plain addition, and
twenty units in the case of addition with carriage.
60
Beyond this, there were certain other operations which
would take extra time; operation and variable cards had
 to be read, the Barrels had to be set, and so on. In
order to accommodate these operations, it in fact took
six cycles to add two numbers. However, the machine was
so arranged that in certain circumstances it could perform
different operations simultaneously in different sections;
in a series of additions, it was possible to add each
additional number after the first two in a single extra
cycle. In other words, adding (or subtracting) n numbers
together in succession, each of forty digits, would
require n + 4 cycles of twenty units.
to be read, the Barrels had to be set, and so on. In
order to accommodate these operations, it in fact took
six cycles to add two numbers. However, the machine was
so arranged that in certain circumstances it could perform
different operations simultaneously in different sections;
in a series of additions, it was possible to add each
additional number after the first two in a single extra
cycle. In other words, adding (or subtracting) n numbers
together in succession, each of forty digits, would
require n + 4 cycles of twenty units.
As to the length of the unit of time, wishing to give
a conservative estimate of the speed of the Engine, Babbage
estimated the maximum practicable velocity of the circumference
of the figure wheels as ten feet per minute, or
two inches per second; this would give a unit of time
about 0.157 seconds long. Thus a cycle of twenty units
would be about 3.14 seconds. This would mean that adding
two numbers together would take about 18.8 seconds, but
that each additional number would require only another
3.14 seconds.
61
In the case of multiplication and division, the time
required depended on the number of digits in the numbers
being operated on, and Babbage's own calculations of the
time needed were incomplete; but seemingly for two
numbers of about forty and twenty digits respectively,
 for example, multiplication would have required a little
less than two minutes, with division taking somewhat
longer.
62
for example, multiplication would have required a little
less than two minutes, with division taking somewhat
longer.
62
It will be readily apparent that the above mentioned
ten unit cycle is a theoretical minimum for addition only
in the case of decimal operation, and that there would be
a different cycle length for different numerical bases;
this was also apparent to Babbage. His initial concern
was that the performance of carriage was - even after
all the work on it - still taking a large fraction of
the total time. Babbage calculated that carriage
would take only about one ninth as long if the Mill were
operated on a numerical base of one hundreds but he
decided not to adopt this base.
63
In general, the length
of the basic cycle would vary directly with the magnitude
of the base, but the number of cycles needed for
multiplication or division would vary inversely with the magnitude
of the base used. This general problem led Babbage to
consider the question of "whether an arithmetic whose
basis were 12, 16 or any other number being adopted, the
operations might not be performed in a shorter time,
notwithstanding the time consumed in converting the numbers
out of the decimal scale and in reconverting the results
 into that scale."
64
Babbage did not record the reasoning
which he went through, but he decided to continue his
planning on a decimal basis.
into that scale."
64
Babbage did not record the reasoning
which he went through, but he decided to continue his
planning on a decimal basis.
The modern reader, concerned with the relation of
what Babbage did to modern computers, would be interested
primarily in evidence that Babbage considered using the
binary system. It must be bone in mind, however, that
the binary system is used in modern machines primarily not
because of any inherent superiority or logical purity
it has in comparison to other bases, but because the
components of which modern machines are constructed, being
electronic or magnetic, are themselves inherently binary, and
in this respect less flexible than Babbage's wheels.
In any case there is some evidence that Babbage was
considering some use of the binary system in the Engine.
While discussing Number and Variable Cards in his December,
1837 paper, he remarked that "fourteen levers and their
equivalent fourteen holes will be all that is required . . .
for eight thousand variables."
65
Unfortunately the context
does not make very clear what Babbage was talking about,
but the fact that 213 equals 8192 strongly suggests that
Babbage was pointing out that fourteen binary bits -
 represented by fourteen possible holes in a card -
could convey numbers up to eight thousand to the machine,
with the fourteenth hole serving to convey the sign.
Later, however, Babbage planned simply to have a
different hole punched out for each of the digits from
one to nine.
66
represented by fourteen possible holes in a card -
could convey numbers up to eight thousand to the machine,
with the fourteenth hole serving to convey the sign.
Later, however, Babbage planned simply to have a
different hole punched out for each of the digits from
one to nine.
66
We have thus seen the picture of the internal
development and operation of the Analytical Engine
that emerges from an examination of Babbage's working
notebooks and drawings, and from his December, 1837 paper.
By this point Babbage had completed the invention of what
we now know as the general purpose digital computer, and
thus the changes which he worked on in later years were -
by definition - not changes in principle, but rather
changes to speed up the operation of the machine, or
make it easier to construct, or some other such practical
matter. Before proceeding with any further mechanical
details, it will be well to consider the Engine in a
more general context, in terms both of Babbage's own
attitude toward it, and the communication concerning it he
had with the outside world, in which that attitude is
sometimes clearly revealed.

One aspect of this has already been covered in Chapter
Two, namely the communication respecting the Analytical
Engine which Babbage had with the government in
connection with their support for the construction of
the Difference Engine. It will be remembered that in
his statement to the Duke of Wellington dated December 23,
1834, Babbage had announced the invention of a new machine
with far greater powers than the Difference Engine, but
one which did not supersede it,
67
1836 Babbage was saying that the old machine had been
rendered wholly obsolete.
68
In the first few years of Babbage's work on the
Analytical Engine, he carried on almost no correspondence
concerning it with his friends and colleagues, or at least
almost none is preserved. One notable exception is a
letter written to an unnamed friend (apparently an
American), dated August 2, 1835.
69
In this letter, Babbage
described how, on gaining access to his drawings of the
Difference Engine the previous September, a re-examination
of them had led him to the invention of a new machine at
the same time more powerful and less complex than the old
one. He continued:
I have had a draftsman constantly at work since
September and I have given up all other pursuits for
 the sake of this, and the progress I have already
made surpasses my expectation, it is indeed more than
I ever before made in several years. This arises
partly from a more enlarged experience, partly by
having a better tempered draftsman, partly by having
all my drawings in my own house instead of at a
distance of four miles. My intention is to finish
a complete set of mechanical drawings of the new
engine and a variety of Mechanical Notations to
explain its operation. I have already got over all
the difficulties of the first order and most of those
of the second and feel very confident that in twelve
months more, if I can carry it on as I have done, that
I shall have completed the drawings so that the
invention can not ever be lost.
70
the sake of this, and the progress I have already
made surpasses my expectation, it is indeed more than
I ever before made in several years. This arises
partly from a more enlarged experience, partly by
having a better tempered draftsman, partly by having
all my drawings in my own house instead of at a
distance of four miles. My intention is to finish
a complete set of mechanical drawings of the new
engine and a variety of Mechanical Notations to
explain its operation. I have already got over all
the difficulties of the first order and most of those
of the second and feel very confident that in twelve
months more, if I can carry it on as I have done, that
I shall have completed the drawings so that the
invention can not ever be lost.
70
Babbage then gave a brief outline of the function
of the new machine, mentioning that among other things
it could extract the roots of numbers by successive
approximations, calculate logarithms and Bernoulli
numbers, sum converging series, and reduce large numbers
of observations.
Babbage concluded this letter as follows:
You will be able to appreciate the influence of
such an engine on the future progress of science. I
live in a country which is incapable of estimating
it and I am much displeased with the treatment
I have experienced . . . I have made large sacrifices
and am prepared to make still larger. There is
however, a limit at which my duty to my children
demands my forbearance and I place that at the
completion of my drawings, which is in fact the
completion of the invention. These will remain when
I am gone, and when some more enlightened country
than my own shall at some future period become sensible
of the value of the engine or ambitious of the fame
of calling it into real existence, those drawings
will undoubtedly be sought and from them a machine
will be made which shall give to all nations and to
 all after time, tables at once perfect and enduring,
and which shall execute calculations from which all
human agents would shrink in hopeless despair. I
have thus given you an outline of the work I am
employed in; the views that it has opened and which
it continually suggests are amongst the most
interesting and important I have met with.
71
all after time, tables at once perfect and enduring,
and which shall execute calculations from which all
human agents would shrink in hopeless despair. I
have thus given you an outline of the work I am
employed in; the views that it has opened and which
it continually suggests are amongst the most
interesting and important I have met with.
71
It is notable in this passage that Babbage was still
thinking at this time, August 1835, in terms of the
production of tables as the primary function of the new
machine. This idea was one that Babbage was to continue
to hold and express for many years, and this was true also
of several other themes laid out in the same passage, for
example that the machine could not be properly appreciated
in England, and that he himself would not build it, but
that it would be built after his death, and have a profound
influence upon science.
This last point particularly was amplified and
powerfully expressed in the passage with which Babbage concluded
his paper of December 26, 1837, from which extensive
quotation has already been made; the final paragraph
read:
72
Whenever engines of this kind exist in the
capitals and universities of the world, it is obvious
that all those enquirers who wish to put their theories
to the test of number will apply their efforts so
to shape the analytical results at which they have
arrived that they shall be susceptible of calculation
by machinery in the shortest possible time, and the
whole course of their analysis will be directed
towards this object. Those who neglect the indication
will find few who avail themselves of formulae whose
 computation requires the expense and the error
attendant on human aid.
computation requires the expense and the error
attendant on human aid.
In the same paper, Babbage felt for the first time
the need to express the opposite idea, namely that the
machine had limitations; the form in which this was
expressed is particularly interesting, for it came close
to speaking directly to the modern worry over whether or
not a machine can "think." In the passage in question,
Babbage was apologizing in a footnote for the use of
expressions like "the engine knows" or "the engine forsees"
something. He said:
In Substituting mechanism for the performance
of operations hitherto executed by intellectual
labor it is continually necessary to speak of
contrivances by which certain alterations in parts of
the machine enable it to execute or refrain from
executing particular functions. The analogy between
these acts and operations of mind almost forced upon
me the figurative employment of the same terms. They
were found at once convenient and expressive, and I
prefer continuing their use rather than substituting
lengthened circumlocutions. For instance, the
expression "the engine knows etc." means that one
out of many possible results of its calculations has
happened and that a certain change. has taken place
by which it is compelled to carry on the next
computation in a certain appointed way.
73
Despite the large amount of time Babbage was putting
into the planning of the new calculating machine in the
next couple of years,
74
his correspondence still did not
 discuss the Engine. Yet apparently this was despite a
growing commitment to it, for on December 26, 1838, Babbage
wrote to the Vice Chancellor of Cambridge University,
communicating his desire to resign from the Lucasian
Professorship, this sacrifice being necessary for the
sake of "the completion of the designs and description of
the Calculating engine."
75
discuss the Engine. Yet apparently this was despite a
growing commitment to it, for on December 26, 1838, Babbage
wrote to the Vice Chancellor of Cambridge University,
communicating his desire to resign from the Lucasian
Professorship, this sacrifice being necessary for the
sake of "the completion of the designs and description of
the Calculating engine."
75
Not until December, 1839, can one find another letter
of interest concerning the machine; on that date, Babbage
wrote to the noted French scientist D.F.J. Arago in Paris,
asking Arago to get for him a copy of the portrait of
Jacquard woven on the Jacquard loom, an example of which
Babbage had recently seen in London. He gave the following
account of why he was anxious to get the portrait:
You are aware that the system of Cards which
Jacquard invented are the means by which we can
communicate to a very ordinary loom orders to weave
any pattern that may be desired. Availing myself of
the same beautiful invention, I have by similar means
communicated to my Calculating engine orders to
calculate any formula however complicated. But I
have also advanced one stage farther, and without
making all the cards, I have communicated through the
same means orders to follow certain laws in the use
of those cards, and thus the Calculating Engine can
solve any equations, eliminate between any number of
variables, and perform the highest operations of
analysis. Imagine then that I am anxious to possess
so singular a portrait of your distinguished countrymen.
76

Babbage concluded this letter with the following
account of this progress:
I am continuing unintermittedly the Drawings of the
machine on which I was engaged when you last visited
London. I hope at my own expense and by my own
efforts to leave behind me the drawing and full
descriptions of an engine which has the power of
solving by mere mechanical means most of the great
problems of analysis.
In the original draft, this last sentence continued with
the following words, subsequently struck out:
But it is very improbable that I shall ever possess
the pecuniary means to undertake its execution. I
have spent many thousands of my private fortune on
this pursuit, and when the drawings are completed,
the invention can never be lost.
77
In 1840, Babbage received an invitation from the
Italian mathematician Giovanni Plana to attend the second
Riunione degli Scienziati Italiani, to be held in Turin
in September, where all the leading Italian scientists
would meet. The year before, Babbage had declined an
invitation to attend the first meeting, on the grounds
that it would hinder the progress of the Analytical
Engine.
78
In 1840, however, Babbage changed his mind,
doubtless in part because of the interest Plana had expressed
in his invitation:
M. Plana stated that he had inquired anxiously
of many of my countrymen about the power and mechanism
of the Analytical Engine. He remarked that from
all the information he could collect the case seemed
to stand thus:

"Hitherto the legislative department of our
analysis has been all-powerful - the executive all
feeble.
"Your engine seems to give us the same control
over the executive which we have hitherto only
possessed over the legislative department."
79
Babbage was very taken with this expression of the
possibility that the Analytical Engine could make aspects
of analysis which had previously been of purely theoretical
interest become practical and useful. He decided to go to
Turin, for the following reasons:
The great object of my visit to Turin was to convey
to Plana and to some of the Analysts of Italy the
principles on which I had contrived an engine to
perform as he has beautifully expressed it "the
whole Executive of Analysis." The discovery is so
much in advance of my own country and I fear even
of the age, that it is very important for its
success that the fact should not rest on my own
unsupported authority. I therefore selected the
meeting at Turin as the time of publication, partly
from the celebrity of its Academy and partly from my
high estimation of Plana.
80
Babbage took with him to Italy "such of my models,
drawings and notations as I conceived to be best
adapted to give an insight into the principles and modes
of operating of the Analytical Engine." At Turin, while
the regular scientific meetings were in recess, Babbage
met privately with Plana "and others of the most eminent
geometers and engineers of Italy." Among these
 "others" was Luigi Federico Menabrea.
"others" was Luigi Federico Menabrea.
 Babbage later
described these meetings as follows:
82
Babbage later
described these meetings as follows:
82
These discussions were of great value to me
in several ways. I was thus obliged to put into
language the various views I had taken, and I
observed the effect of my explanations on different
minds. My own ideas became clearer, and I profited
by many of the remarks made by my highly-gifted
friends.
Babbage hoped that as a result of his visit to
Turin, Plana would give a report on the Analytical Engine
to the Academy of Turin, so that its importance would
not rest on his own unsupported authority. However,
Plana became ill, and the paper did not get written.
In March, 1841, Babbage wrote to Angelo Sismonda, suggesting
that one of the other people, including Menabrea, who had
heard his exposition could assist in drawing up the
report.
83
In about July, 1841, Babbage wrote to Alexander
von Humbolt, whom he had known for many years:
I am very desirous to make you acquainted
with the object that I have proposed to accomplish
and to convince you that the means exist of
constructing an engine which as Plana has described
it gives us as complete a power over the executive
of analysis as we have hitherto possessed over the
legislative portion. The greater part of the drawings exist
 by which an engine might be made which shall reduce
to numbers any explicit function whose laws of
formation can be assigned. For instance, the
equation of finite differences expressing the law of
formation of the numbers of Bernoulli being given
to it, it will work out and print the successive
numbers.
by which an engine might be made which shall reduce
to numbers any explicit function whose laws of
formation can be assigned. For instance, the
equation of finite differences expressing the law of
formation of the numbers of Bernoulli being given
to it, it will work out and print the successive
numbers.
This engine is unfortunately far too much in
advance of my own country to meet with the least
support. I have at an expense of many thousand
pounds caused the drawings to be executed, and I
have carried on experiments for its perfection.
Unless however some country more enlightened than
my own should take up the subject, there is no chance
of that machine ever being executed during my own
life, and I am even doubtful how to dispose of these
drawings after its termination.
84
Babbage went on to say that he was most anxious to explain
the machine to Humbolt and to get his advice, but that as
the material needed for the explanation could not readily
be taken abroad, he would have to invite Humbolt to visit
London to see it.
One other point about this letter must be mentioned;
it is apparently the first place in which Babbage used
the term "analytical engine" although in this instance
it does not seem to have taken on the role of a proper
name for the machine, it did so shortly after.
85
Although
there is no direct evidence, it seems likely that Babbage
came to use this name because of the phrase from Plana's
letter to him of 1840, which he quoted quite frequently,
 to the effect that the machine would allow man's
"legislative" power over analysis to be extended to
include "executive" power: this relation was then
summarized in the term Analytical Engine.
to the effect that the machine would allow man's
"legislative" power over analysis to be extended to
include "executive" power: this relation was then
summarized in the term Analytical Engine.
Nothing came of this attempt to gain Humbolt's
backing for the Analytical Engine, but apparently
Babbage desired it for two main reasons. First, he felt
he was unlikely to get understanding and support for
the machine from his own countrymen. Second, he wanted
support for his ideas at this time because he was about
to re-open negotiations with the government over the
Difference Engine, and try to persuade them to underwrite
the Analytical Engine.
86
This is further revealed in a
letter from Babbage to Plana, dated October 3, 1841, in
which he discussed the description of the Analytical
Engine which had finally been drawn up by Menabrea.
Babbage said:
If you had made a report on the subject (of
the Analytical engine) to the Academy of Turin during
the last year it might have been of essential service
to me in the discussion of the question with my own
Government. As it is I must be content with the
description drawn up by M. Menabrea, with which I
am well satisfied because he seems to have penetrated
completely the principles on which it rests.
87
Menabrea's paper was published in October, 1842
in French, and later in English, and will be discussed
 below. Evidently, however, Babbage was not as "well
satisfied" as he might have been, for on October 7, 1841,
having finally succeeded in getting an account of the
Analytical Engine written by someone else, he set about
writing another of his own.
below. Evidently, however, Babbage was not as "well
satisfied" as he might have been, for on October 7, 1841,
having finally succeeded in getting an account of the
Analytical Engine written by someone else, he set about
writing another of his own.
This 1841 paper, called "Of the Analytical Engine,"
88
was a fairly straightforward introduction to the Analytical
Engine on an elementary level, rather similar to the 1837
paper discussed and quoted extensively earlier in this
chapter, though not as polished or complete. It did not,
for example, go any further into the principles of the
Combinatorial Cards or their mode of action, the cards
which would have controlled in detail the flow of
instructions into the Mill.
What was valuable about the 1841 paper was its
introduction, where Babbage set out in a much clearer
and more coherent way his conception of the general
character of the Analytical Engine. This introduction
began as follows:
The object of this engine is twofold. 1st
To convert into numbers and to print the results
of any formulae which may be required. 2nd To
develop any analytical formulae the laws of whose
formation are given.
In order to accomplish these objects it is
necessary that it should be possible; lst To
 express in the engine any functions whatever of any
number of quantities and their numerical
magnitude, together with their numerical coefficients,
their indices of operation and their algebraic
signs. 2ndly That it should be capable of performing
with those numbers the four operations of arithmetic.
3rdly That it should be capable of all those
combinations of symbols which the laws of analysis
may require.
express in the engine any functions whatever of any
number of quantities and their numerical
magnitude, together with their numerical coefficients,
their indices of operation and their algebraic
signs. 2ndly That it should be capable of performing
with those numbers the four operations of arithmetic.
3rdly That it should be capable of all those
combinations of symbols which the laws of analysis
may require.
After stating what the Analytical Engine will
do it may perhaps be necessary to state what it
cannot accomplish. It cannot invent. It must
derive from human intellect those laws which it
puts in force in the developments it performs.
It cannot in fact do anything more than perform with
absolute precision and in much shorter time those
series of operations which the hand of man might
itself much more imperfectly accomplish. It must
however be observed on the other hand that this great
abridgement of time does in a certain sense render
possible calculations which otherwise might be
practically although not physically impossible from
their tediousness as well as expense.
Another and an important fact is that it will
perform calculations which the hand of man has
never yet attempted, such as the elimination of one
variable between two equations of the 6th dimension,
and that in communicating to it our commands to
execute such operations, it is quite unnecessary that
we should ourselves go through them even in the
first instance. This is accomplished by communicating
to it the laws according to which the system of
operations is performed.
89
In the rest of the introduction to his 1841 paper,
Babbage discussed the possibility of actually constructing
a machine with the powers described. Without making any
remarks as to his own plans or intentions about building a
working machine, he set out three prerequisites for the
construction of an analytical engine.

First, it must "be possible to carry on the whole
of the executive department of analysis by means of the
combination of a few simple arithmetical and algebraical
processes." Second, it must be the case that "those
elementary principles can be fully effected by means
purely mechanical." Babbage said that the fulfillment
of these pre-conditions was a matter of demonstration,
not of opinion; and although he did not set out to
prove them, he clearly did not consider them to be in doubt.
The third condition was of a different sort. "Whether
that system of contrivances which has been drawn can in
the present state of mechanical art be executed so as to
work regularly and exactly is an important point, a
point on which opinions may fluctuate until experiment
has decided the question." But Babbage expressed his
confidence that "no man thoroughly acquainted with the
present state of machinery in England and having complete
drawings and notations of the engine can or will fail
in making it work perfectly."
90
As mentioned above, L.F. Menabrea had, by October,
1841 written up a description of the Analytical Engine
as described by Babbage in Turin in September, 1840, and
this description was shown to Babbage. For reasons that
 are not clear, it was not published until an additional
year had passed; it is possible that some changes or
additions suggested by Babbage delayed the matter. In
any case, it appeared under the title "Notions sur la
machine analytique de M. Charles Babbage" in the
Biblioteque Universelle de Geneve in October, 1842,
91
and constituted the first published description of the
Analytical Engine.
are not clear, it was not published until an additional
year had passed; it is possible that some changes or
additions suggested by Babbage delayed the matter. In
any case, it appeared under the title "Notions sur la
machine analytique de M. Charles Babbage" in the
Biblioteque Universelle de Geneve in October, 1842,
91
and constituted the first published description of the
Analytical Engine.
In the summer of 1843, Menabrea's paper was translated
by Ada Augusta, Countess of Lovelace, and only legitimate
daughter of Lord Bryon; she composed, in extensive
consultation with Babbage, a series of long notes to the
paper, which together comprised about three times the
length of Menabrea's original version. The whole was
published in Richard Taylor's Scientific Memoirs for 1843,
92
under the title "Sketch of the Analytical Engine invented
by Charles Babbage, Esq;" this was the only extensive
paper on the Analytical Engine published in English
during Babbage's life, or, indeed, up to the present.
Although it is clear that Lady Lovelace was a woman
of considerable interest and talent, and it is clear that
she understood to a very considerable degree Babbage's
ideas about the general character and significance of the
 Analytical Engine, and expressed them well in her notes to
Menabrea's paper, it is equally clear that the ideas
were indeed Babbage's and not hers; indeed, she never
made any claim to the contrary. She made a considerable
contribution to publicizing the Analytical Engine, but
there is no evidence that she advanced the design or theory
of it in anyway. And she did not even express an interest
in learning about the machine until January 5, 1841,
93
even as late as June 30, 1843, she apparently knew quite
little about the mechanical details of the Engine.
94
Analytical Engine, and expressed them well in her notes to
Menabrea's paper, it is equally clear that the ideas
were indeed Babbage's and not hers; indeed, she never
made any claim to the contrary. She made a considerable
contribution to publicizing the Analytical Engine, but
there is no evidence that she advanced the design or theory
of it in anyway. And she did not even express an interest
in learning about the machine until January 5, 1841,
93
even as late as June 30, 1843, she apparently knew quite
little about the mechanical details of the Engine.
94
All of this is said not to belittle Lady Lovelace,
but because a very exaggerated view has been formed by
some recent writers of the significance of her contribution
to the Engine or of her role in Babbage's life.
95
From the present perspective, the Menabrea paper and
the Lovelace notes are more interesting as an actual
 publication on the Analytical Engine than as a source
of additional information. Very little was said of the
operation or mechanical details of the Engine, far
less than in the earlier Babbage manuscript papers.
However, the extent of the powers of the machine, and.
its limitations, and thus the question of its significance,
were developed more clearly and elegantly than in the
earlier works. Menabrea said the following:
publication on the Analytical Engine than as a source
of additional information. Very little was said of the
operation or mechanical details of the Engine, far
less than in the earlier Babbage manuscript papers.
However, the extent of the powers of the machine, and.
its limitations, and thus the question of its significance,
were developed more clearly and elegantly than in the
earlier works. Menabrea said the following:
Considered under the most general point of
view, the essential object of the machine being to
calculate, according to the laws dictated to it,
the values of numerical coefficients which it is then
to distribute appropriately on the columns which
represent the variables, it follows that the
interpretation of formulae and of results is beyond its
province, unless indeed this very interpretation be
itself susceptible of expression by means of the
symbols which the machine employs. Thus, although
it is not itself the being that reflects, it may yet
be considered as the being which executes the
conception of intelligences. . . .Who can foresee
the consequences of such an invention? In truth,
how many precious observations remain practically
barren for the progress of the sciences, because
they are not powers sufficient for computing the
results! And what discouragement does the
perspective of a long and arid computation cast
into the mind of a man of genius, who demands time
exclusively for meditation, and who beholds it
snatched from him by the material routine of
operations! Yet it is by the laborious route of
analysis that he must reach truth; but he cannot
pursue this unless guided by numbers; for without
numbers it is not given us to raise the veil which
envelopes the mysteries of nature. Thus the idea of
constructing an apparatus capable of aiding human
weakness in such researches, is a conception which,
being realized, would mark a glorious epoch in the
history of the sciences.
96

In the notes, these ideas were developed further
and cast in more general terms:
The bounds of arithmetic were. . . . outstepped
the moment the idea of applying the cards had
occurred; and the Analytical Engine does not
occupy common ground with mere "calculating machines."
It holds a position wholly its own; and the
considerations it suggests are most interesting in
their nature. In enabling mechanism to combine
together general symbols in successions of unlimited
variety and extent, a uniting link is established
between the operations of matter and the abstract
mental processes of the most abstract branch of
mathematical science. A new, a vast, and a powerful
language is developed for the future use of analysis,
in which to wield its truths so that these may become
of more speedy and accurate practical application for
the purposes of mankind than the means hitherto in
our possession have rendered possible. Thus not
only the mental and the material, but the theoretical
and the practical in the mathematical world, are brought
into more intimate and effective connexion with each
other. We are not aware of its being on record that
anything partaking in the nature of what is so well
designated the Analytical Engine has been hitherto
proposed, or event thought of, as a practical
possibility, any more than the idea of a thinking or
of a reasoning machine.
97
The Analytical Engine has no pretensions
whatever to originate anything. It can do whatever
we know how to order it to perform. It can follow
analysis but it has no power of anticipating any
analytical relations or truths. Its province is to
assist us in making available what we are already
acquainted with. This it is calculated to effect
primarily and chiefly of course, through its executive
faculties; but it is likely to exert an indirect and
reciprocal influence on science itself in another
manner. For, in so distributing and combining the
truths and the formulae of analysis, that they may
become most easily and rapidly amenable to the
mechanical combinations of the engine, the relations
and the nature of many subjects in that science are
necessarily thrown into new lights, and more
profoundly investigated.
98

The publication of the Menabrea paper and of the
much expanded Lovelace translation and notes was quite
pleasing to Babbage. The former (which Babbage had gone
to Turin in order to bring into being) he considered to
be a "lucid and admirable description" of the Analytical
Engine; the notes Babbage considered to have "entered
fully into almost all the very difficult and abstract
questions connected with the subject." The paper and
notes taken together, said Babbage, "furnish, to those
who are capable of understanding the reasoning, a complete
demonstration That the whole of the developments and
operations of analysis are now capable of being executed
by machinery."
99
Also highly pleased by the translation and notes was
Lady Lovelace, and she was even more pleased with herself
for having produced them, despite what she considered to
have been the inaccuracy and unreliability of Babbage's
revision and suggestions.
100
On July 30, 1843 she wrote
to Babbage, among other things, "The more I study the more
irresistible do I feel my genius to be. I do not believe
that my father [Lord Byron] was (or ever could have been)
such a Poet as I shall be an Analyst (and Metaphysician)."
101

In another letter to Babbage, on August 11, 1843,
Lady Lovelace expressed her goal in life as follows.
"I wish to add my mite toward expounding and interpreting
the Almighty and His laws and works, for the most effective
use of mankind, and certainly I should feel it no small
glory if I were enabled to be one of His most noted
prophets . . . in this world." Apparently this humble
desire was to be fulfilled by Lady Lovelace becoming the
general director of the execution of a working Analytical
Engine. Babbage would promise to confine his attention
entirely to the actual construction of the machine and
"to abide wholly by the judgement of myself . . . whenever
we may differ on all practical matters relating to whatever
can involve relations with any fellow creature or fellow
creatures." Exactly what scheme Lady Lovelace had in mind,
or how she intended to finance it, she would not say, but
in any case the matter was never followed up.
102
Babbage's descriptions of the Analytical Engine
written in 1837 and 1841, discussed earlier, were doubtless
drafts of intended publications, and in December, 1842,
Babbage had sent to a friend for his opinion a collection
of papers which he was considering making into a book on
the Difference and Analytical Engines;
103
however, with
 the appearance of the Menabrea-Lovelace paper, Babbage
evidently felt satisfied, for he published nothing on his
own, and did not try to write any other papers on the
machines for many years. In 1846, he gave as a further
reason for his never having published anything on the
Analytical Engine "the maxim of never employing my
faculties on any but what I consider the highest objects
as long as they are capable of advancing them," the
completion of the plans of the Analytical Engine being
such a "highest object".
104
the appearance of the Menabrea-Lovelace paper, Babbage
evidently felt satisfied, for he published nothing on his
own, and did not try to write any other papers on the
machines for many years. In 1846, he gave as a further
reason for his never having published anything on the
Analytical Engine "the maxim of never employing my
faculties on any but what I consider the highest objects
as long as they are capable of advancing them," the
completion of the plans of the Analytical Engine being
such a "highest object".
104
We have seen how Babbage's conception of the general
character and possible applications of the Analytical
Engine developed from 1834 on, and also the measures that
he took to bring the new machine into public view,
although he preferred that this be done through some other
author, and, indeed, that it first be made public in a
foreign country. We must now survey the practical work
and development that was done during the ten years
following the point in 1837 at which the state of the
Analytical Engine was described earlier in this chapter.
The principle point that must be kept in mind in
considering this development is that Babbage had no plans
 for actually constructing the Analytical Engine in the
immediate future; indeed, as we have seen, he several
times expressed the opinion that it would not be constructed
during his lifetime. This meant that he felt himself
to be under no temporal pressure or restraint, and thus
free to pursue the consequences of any conceivable
modification in the parts of the Engine to their most
remote consequences; usually this was to see if the change
would save any time. Further, he would often take up
consideration of some contrivance which he had rejected
some years before, to see if it would work any better
in relation to some other device or change he was now
considering.
for actually constructing the Analytical Engine in the
immediate future; indeed, as we have seen, he several
times expressed the opinion that it would not be constructed
during his lifetime. This meant that he felt himself
to be under no temporal pressure or restraint, and thus
free to pursue the consequences of any conceivable
modification in the parts of the Engine to their most
remote consequences; usually this was to see if the change
would save any time. Further, he would often take up
consideration of some contrivance which he had rejected
some years before, to see if it would work any better
in relation to some other device or change he was now
considering.
This mode of proceeding on Babbage's part has the
unfortunate consequence that the great majority of the
work he did after 1837 is very uninteresting; it has the
character of neither being a theoretical or practical
breakthrough, nor of leading up to or at any point
constituting any single complete, coherent and final design
for the Analytical Engine, for, as mentioned, Babbage
was under no pressure to come up with such a final
design. Thus most of this work will not be covered in
this thesis. But examples of how this kind of
consideration could lead down both fruitful and useless
paths will be provided, and a few ideas that are
interesting because of their similarities to methods used
 in modern computers will be described.
in modern computers will be described.
One point that needs to be made clear is that the
tendency of what might be called Babbage's perfectionist
approach was not simply to make the machine more complex;
rather there was always a conflicting pull between
simplicity and effectiveness, say in speeding up the
operation of the machine; for Babbage found simplicity
of structure or operation for a device able to do a
certain job (which we might call efficiency) to be just as
theoretically satisfying as raw capacity in itself; and
he always thought of himself as working on a machine that
would eventually be built.
Babbage described these conflicting tendencies very
clearly in describing the difference in approach to the
Great Analytical Engine on which he was working before the
trip to Turin in September, 1840, and the simplified
Small Analytical Engine which he began after this trip.
105
In fact, although the description pictured these as two
diverse enterprises, the distinction was not maintained in
his own work, and the same two approaches were battling
each other in everything he did. As Babbage said:
The principles on which the great Calculating
Engine was designed and drawn were:
1 That it should execute all its operations
in the smallest possible time. This was the great
 guiding principle and even single turns of the hand
were considered.
guiding principle and even single turns of the hand
were considered.
2nd That although the mechanism employed should
be as simple as could be contrived, yet in no case
should simplicity be purchased at the expense of
time, provided the mechanism was of such a kind
that it could in the present state of mechanical
art be successfully executed.
3rd Expense of construction was never to be
considered; whatever plan was thought to be the
shortest in time, possible in execution and durable
in structure was always adopted.
106
In the Small Analytical Engine on the other hand, the
approach was quite different:
The great object for which this was undertaken
was to reduce the cost of construction to such a
moderate sum as might render it possible that it might
be executed.
The guiding principle was to give up all the
more complicated mechanism, especially that which
only effected small savings of time, and even if
necessary some of the larger savings when they
required great expense.
107
It may well be that Babbage decided to make the plans
more practical as a result of the enthusiastic reception
his ideas met with in Turin. But in fact, the distinction
between Great and Small engines became one between two
phases of his thinking through any given new idea. Babbage
would go to extreme lengths to see if the idea would save
any time; if it would, he would work on it in an attempt
to simplify the mechanism necessary for him to adopt it
 in the machine. When this was done, he would consider
the complexity of the device in relation to the time
saved; if it was large, he would reject the device;
if it was small, he would adopt it. Frequently, however,
the efficiency of the device would be ambiguous, so that
Babbage could not decide whether to adopt it or not.
in the machine. When this was done, he would consider
the complexity of the device in relation to the time
saved; if it was large, he would reject the device;
if it was small, he would adopt it. Frequently, however,
the efficiency of the device would be ambiguous, so that
Babbage could not decide whether to adopt it or not.
An example of this process, which also illustrates
the very complex trains of thought through which Babbage's
mind worked over long periods of time, is the technique
Babbage called Half Zero Carriage. It will be recalled
that in his 1837 paper on the Analytical Engine, Babbage
had believed that the theoretical minimum time necessary
for adding a decimal digit in the machine would be ten
units of time, where the unit was defined as the time
needed for a figure wheel to turn from one digit to the
next.
108
In the 1837 plans, the same minimum time was
necessary for clearing a column, that is, reducing all its
wheels to zero, by the method described earlier.
The Small Analytical Engine, as was said, was begun
in November, 1840. One of the first crucial questions was
whether to continue using multiplication and division by
table (which required a lot of complex mechanism for the
table axes and selection apparatus), or to go back to the
 earlier and much simpler method of multiplication and
division by repeated addition and subtraction; the latter
method, however, would make the machine much slower,
requiring as much as seventeen minutes for division of
sixty figures by thirty figures.
109
earlier and much simpler method of multiplication and
division by repeated addition and subtraction; the latter
method, however, would make the machine much slower,
requiring as much as seventeen minutes for division of
sixty figures by thirty figures.
109
The first thing Babbage realized was that he could
reduce the number of table axes needed to five by the
following method. On five axes were placed the first
five multiples of the multiplicand; if a given digit of
the multiplier was less than five, the selecting mechanism
would enter the corresponding multiple in the usual way.
If a digit greater than five was presented to the selecting
mechanism, it had to, as Babbage put it, "move back from
the fifth multiple by a number equal to the excess of that
digit above five," that is, by the tens complement of
the specified digit. The multiple corresponding to this
complement was then subtracted from the result column, and
the next higher digit of the multiplier was increased by
one.
110
This new form of multiplication would have allowed
Babbage to reduce the number of table axes to five for
the Small Analytical Engine, but it would have also made
the process as a whole, particularly the problems of
selection and control, much more complicated. This did not
 cause Babbage to abandon it, however, for it began to
suggest things more interesting to him than the simplification
which he had set out on.
cause Babbage to abandon it, however, for it began to
suggest things more interesting to him than the simplification
which he had set out on.
On December 15, 1840, Babbage noticed that in one
stage of the multiplication process he had accidentally
allowed only five units of time for clearing a carriage
column from a previous operation (this clearing was
overlapping with another part of the operation), whereas
the clearing required ten units.
111
Instead of lengthening
the cycle by five units, Babbage reflected that it took
ten units to clear a wheel only because if it stood at
nine, it would have to be turned all the way around to get
back to zeros but if it were turned back the shortest
way, that is, in the other direction if the wheel stood
at a number above five, then it would take only five
units. This method Babbage called clearing by "Half Zero,"
seemingly because the zero stood in the middle of the
segment through which the wheel might be turned in clearing
it.
112
It was also clear that a similar method could be
used for transferring a number from one column to another
whose wheels all stood at zero; at first he intended to
do this by putting the same number on two different axes,
each to be turned one way, but this was not necessary.
113

However, these ideas suggested to Babbage a method
for a new process of division in which the selection process
was not tentative (that is, subject to reversal of a step
because of a running up), and would thus be faster; the
idea was to place on nine special axes the tens complements
of the nine multiples of the divisor, and make selection
by adding the dividend (or remainder at any given point)
to all of these axes. This addition would cause a running-up
on some of the axes; the number of the highest axis to
run up would give the appropriate digit in the quotients
further, the result of the addition on that same column
would give the remainder at that point in the division;
when this remainder was again added to the complement
axes (after they had been reset), the next digit would be
obtained, and so on.
114
This method of division was sufficiently fascinating
to Babbage that he lost interest in his efforts to devise
a Small Analytical Engine that would be easy to build;
also he continued to develop this and related ideas rather
than that of half-zero figure wheels. In fact it was not
until more than a year later, in April, 1842, that Babbage
went beyond the use of half-zero for reducing columns to
zero, for at this point he realized that he could use half
 zero for reducing the time of addition and subtraction
themselves.
115
zero for reducing the time of addition and subtraction
themselves.
115
This was to be done by a method quite similar to
that used for transferring numbers by half zero (two
reducing arms turning opposite ways), except that the
column receiving the number would not be standing at zero.
The effect of this was that if one number was being added
to another, the digits standing at or below five would
be added in the usual way, while the digits above five
would have their tens complements subtracted; likewise
in subtractions, the digits above five would have their
complements added, while the lower digits would be handled
normally. Again, the intention of all this was to reduce
the basic time needed for these operations (exclusive of
carriage) from nine to five units of time.
The great difficulty with this approach was that it
required a new and much more complicated carriage mechanism,
since the conditions which determined whether or not a
carriage should take place were much more complicated than
in conventional operation. As in the first stage of
development of the Analytical Engine, Babbage considered
using both hoarding and anticipating carriage,
116
and again decided that the latter was preferable.

Another circumstance that was important at this point
was that Babbage had decided that as stepping numbers
up or down only a single cage at a time took too much
time, he wanted to be able to step any number of cages
at once. He rejected the method of having a very large
number of pinions which could be selectively put in
gear (which he had considered back in 1834), since the
number of pinions would have to be proportional to the
square of the number of significant digits; instead he
decided to take a number column and simply move it bodily
up or down the desired number of cages. The great
difficulty was that with his designs at this point, the
columns already were about eight feet high and very
heavy, so that it was not practical to move them around
with any abandon.
117
As the primary obstacle to reducing the height of.
each cage was the size of the carriage mechanism, it
became desirable to redesign the carriage mechanism both
to reduce its size and to make it possible to use
half-zero addition and subtraction.
Babbage went on in the following months and years
to work very extensively on the details of an anticipating
half-zero carriage, and the requirements and possibilities
which his designs brought forth continued to interact with
 and influence in substantial ways the design of the Engine
as a whole. The details of the development will not be
discussed here. It should be noted, however, that at
times, as on August 1, 1845, the difficulties of
half-zero carriage led Babbage to decide to abandon it,
118
although a few months later he was back to making plans
for it.
119
and influence in substantial ways the design of the Engine
as a whole. The details of the development will not be
discussed here. It should be noted, however, that at
times, as on August 1, 1845, the difficulties of
half-zero carriage led Babbage to decide to abandon it,
118
although a few months later he was back to making plans
for it.
119
Rather than plunging further into this morass of
detail, it will be well to cover briefly a few other
important points or threads of development between 1837
and 1847. One subject in particular calls for further
explanation, as the description of it in Babbage's 1837
paper, discussed earlier, leaves much to be desired:
this is the function and operation of the Combinatorial Cards.
The vague explanation of Combinatorial Cards in the
paper dated December 26, 1837, may be accounted for by the
fact that the first statement on the subject in the notebooks
is dated December 13, 1837, and is itself rather vague.
120
Apparently what Babbage envisioned was that there would
be a series of steps in a program which would be repeated
many times at the beginning, and then some additional
steps at the end that would be performed only once
 apiece; Babbage may have had in mind some such thing
as computing a number of terms in a mathematical series,
and then forming their sum. In any case, the plan was to
have a special set of combinatorial counting wheels;
on these would be placed the number of times the special
set of operations at the beginning of the program was to
be repeated. At the end of this set of operation cards
would be a special combinatorial card; when it was reached,
unity would be subtracted from the combinatorial figure
wheels, and the operation cards would be turned back to
the beginning. However, when, after a number of repetitions,
the combinatorial figure wheels read zero, the index card
at the end of the sequence would be ignored, and the Engine
would go on to the next card.
apiece; Babbage may have had in mind some such thing
as computing a number of terms in a mathematical series,
and then forming their sum. In any case, the plan was to
have a special set of combinatorial counting wheels;
on these would be placed the number of times the special
set of operations at the beginning of the program was to
be repeated. At the end of this set of operation cards
would be a special combinatorial card; when it was reached,
unity would be subtracted from the combinatorial figure
wheels, and the operation cards would be turned back to
the beginning. However, when, after a number of repetitions,
the combinatorial figure wheels read zero, the index card
at the end of the sequence would be ignored, and the Engine
would go on to the next card.
Although by May 10, 1838, this plan had become somewhat
more coherent, it had not become more flexible.
121
It
provided only for backing the operation cards to a pre-determined
point, although the number of repetitions could
be varied. On February 9, 1839, Babbage mentioned another
idea, whereby after a series of cards was completed, they
could be turned to a point other than the beginning of
the series; this was done by putting the number of cards
that were to be turned on a special backing apparatus;
when the point was reached where the transfer was to be
 made, the backing apparatus was geared with the card
prism, and then reduced to zero, turning the cards as it
went. The number that was to be put on the backing
apparatus could be either computed internally or specified
in advance by a number card, following the principle which
Babbage was to express two years later in these words:
made, the backing apparatus was geared with the card
prism, and then reduced to zero, turning the cards as it
went. The number that was to be put on the backing
apparatus could be either computed internally or specified
in advance by a number card, following the principle which
Babbage was to express two years later in these words:
Any fact which is certain and known before execution.. .
should be ordered by cards. Any fact which although
equally certain is unknown previously to the actual
working out of the formula should be governed by Mill
or Counting Apparatus, etc.
122
In late March, 1843, Babbage mentioned a method by
which the operation on a single card could be repeated
as many times as desired. Each operation card had punched
on it the number of times it was to be repeated. The
first time it was read, this number was put onto the
card counting apparatus; the card was then used again
to set the barrels, but the index on it was ignored,
unity being subtracted from the card counting apparatus
instead. When the number on it reached zero, the cards
were advanced by one, a new index was taken in, and so
on. It is not clear what this was supposed to accomplish,
but seemingly it simply reduced the number of cards needed
when an operation was to be done many times together, for
this plan did not provide any increased power or flexibility
to the Engine.
123

In November and December of 1843, Babbage spelled
this plan out a bit further. Each operation card was
to be able to convey to a card counting apparatus any
index number less than 1000. In order to save space on
the card, this was to be done in the following way. Each
digit to be conveyed had corresponding to it holes
standing for one, three and nine; the holes for one
and three also had holes to indicate if they were
negative. By combining the digits +1, + 3, and +9, any
digit from zero to nine could be expressed, and thus
numbers up to 999 could be represented by fifteen holes,
rather than thirty. Also, there were to be several
different card counting apparatuses on which the indexes
could be placed; one might control the number of times an
operation was to be repeated, while another would
determine the interval through which the cards were to
be moved after the repetition was complete.
124
Although Babbage continued to consider various minor
modifications of these schemes, the differences were not
important. What can be said is that all the elements
necessary for full flexibility in instruction addressing
were available in the machine. Yet although Babbage was
aware that a variety of repetitions and branchings would
be necessary, he never felt compelled by the kinds of
 programs he got around to considering
125
to make explicit
or coherent any. but simple examples of the methods of
program control.
programs he got around to considering
125
to make explicit
or coherent any. but simple examples of the methods of
program control.
This discussion of the development of the Analytical
Engine beyond the stage described earlier in the chapter
may be concluded with a few examples of developments in
it which are paralleled by features of modern computers.
Perhaps the most interesting is Babbage's thoughts on
the use of what we might call external memory, and
especially the use of pre-computed tables to be consulted
by the machine.
We have already seen how Babbage, as early as March,
1835, had intended to do multiplication (and shortly
thereafter division) by constructing internal tables of
the first nine multiples of the multiplier on special
axes. On August 7, 1837, it occurred to Babbage that he
might similarly form a table of the low integral powers
of the digits one through nine, and that then the first
digit of the corresponding roots of numbers could be found
by working backward through this table.
126
At first it
seems he thought of having this table internal, as with
the multiplication table, although they were substantially
different, in that the multiplication table was specially
 computed for each different multiplier. However, in
early September, 1837, Babbage was considering some
matters connected with having the Engine punch its own
cards, and it occurred to him that he could have the
Engine form tables on cards for its own use. On September.
7 he considered having a table of one hundred cards
corresponding to the digits from one to one hundred,
each having also punched in it the first two digits of
its square root. Then when the Engine wanted the square
root of a number, it would turn through these cards to the
one corresponding to its first two digits, and would then
obtain the first two digits of the square root. In both
these methods subsequent digits would be found by some
method of successive approximations.
127
computed for each different multiplier. However, in
early September, 1837, Babbage was considering some
matters connected with having the Engine punch its own
cards, and it occurred to him that he could have the
Engine form tables on cards for its own use. On September.
7 he considered having a table of one hundred cards
corresponding to the digits from one to one hundred,
each having also punched in it the first two digits of
its square root. Then when the Engine wanted the square
root of a number, it would turn through these cards to the
one corresponding to its first two digits, and would then
obtain the first two digits of the square root. In both
these methods subsequent digits would be found by some
method of successive approximations.
127
Babbage realized that this technique could have
wider applications than the extraction of roots, for on
September 9, 1837, he noted that "possibly several systems
of punched cards might be employed to reduce Astronomical
and barometric observations by."
128
At about the same
time Babbage also considered forming a table of the first
one hundred multiples of a multiplier on cards; the
selecting apparatus would then have turned to the card
corresponding to a given pair of digits, and the multiple
on the card would have been added to the appropriate column.
 This would have halved the number of separate additions
(or subtractions in the case of division) necessary for
a multiplication, and eliminated the need for table axes
in the Mill. However, on September 19, Babbage rejected
the idea, because turning through the string of cards
to get to the right one would have required an inordinately
large amount of time.
129
This would have halved the number of separate additions
(or subtractions in the case of division) necessary for
a multiplication, and eliminated the need for table axes
in the Mill. However, on September 19, Babbage rejected
the idea, because turning through the string of cards
to get to the right one would have required an inordinately
large amount of time.
129
The idea was not followed up until May 22, 1842,
at which point Babbage described a considerably
more elaborate system for having the machine be able to consult
logarithmic tables in the course of its computation.
The machine would itself have computed log tables, and
placed on cards both the argument, with five digits, and
its logarithm, with ten. The complete set of cards with
this table would be placed in a drawer near the Engine.
Then when it wanted a logarithm, it would ring a bell for
the attendant and display the number whose log it wanted;
he would fetch the corresponding card from the drawer
and feed it into the machine. The Engine would then
subtract the argument punched on the card from the number
it had specified, and check that the first five digits of
the result were equal to zero; if they were not, the
Engine would ring "a great bell to tell [the] Assistant
 he had made a mistake."
130
Babbage also intended to
have punched on the same cards the first and second
difference of each logarithm, for use in interpolating
to more than five figures in the argument. He also
realized that the same method would work equally well for
functions other than the logarithm.
he had made a mistake."
130
Babbage also intended to
have punched on the same cards the first and second
difference of each logarithm, for use in interpolating
to more than five figures in the argument. He also
realized that the same method would work equally well for
functions other than the logarithm.
Babbage was quite pleased with this method, not
only because of its usefulness and relative simplicity,
but because a description of the ability of the machine
to know when it had been fed the wrong card, without a
description of the simple means by which this was
accomplished, made it sound as if the Engine had very
peculiar powers. Consequently he gave a lengthy description
of the technique in his book Passages From the Life of a
Philosopher, and added the following very prescient
observations:
It will be an interesting question, which time only
can solve, to know whether such tables of cards
will ever be required for the Engine. Tables are
used for saving the time of continually computing
individual numbers. But the computations to be
made by the Engine are so rapid that it seems most
probable that it will make shorter work by computing
directly from proper formulae than by having recourse
even to its own Tables.
131

Remarkably, despite the tremendous alteration in the
time scale of computation, this "interesting question" is
still relevant today.
One advantage of feeding numbers into the Analytical
Engine in this way was that it eliminated the possibility
of error when wheels had to be set by hand. Babbage
realized that this was equally true for the "formula"
(program), since the great complexity possible in it made
it especially important that it be fully "verified"
(debugged). This made especially valuable the separation
between the operation cards and the variable and number
cards, since it was possible to verify a formula, and then
be confident of its accuracy when at some later time it
was run with some new set of data.
132
It would thus be
possible to build up a "library" of verified formulae which
would be used repeatedly. He also realized that not only
could the Analytical Engine use formula cards that it had
previously verified, or number cards that it had previously
punched, but that one such machine could share its cards
and programs with another, and that therefore a card copying
machine would be useful. He went on to say:
It is desirable that all Analytical Engines should
have cards of the same size. But it is very improbable
that those first used will be of the best size.
Hence in making the card copying machine it will be
necessary to contrive means of changing the punches
 so that Cards may be copied in any given size.
133
so that Cards may be copied in any given size.
133
We may conclude by noting two further minor but yet
interesting ideas that emerged during this period. One
was that it would be desirable to have the Analytical
Engine able to do calculations using pounds, shillings
and pence, although it is not clear what sorts of monetary
calculations Babbage had in mind. Curiously, he intended
to accomplish this by altering the internal hardware of the
machine, rather than by having special formulae for
converting input and output.
134
Another plan to modify the engine so that it could
handle material which required something other than
straightforward numerical output, was that of providing
two extra kinds of cards to control the printing of
results; these served a function essentially identical
to that served by FORMAT statements in current FORTRAN
programming. One set controlled the horizontal and vertical
motion of the paper (or copper plate) on which the results
were printed, while the other would insert such explanatory
symbols and text between the data as was desired.
135
This kind of development, mixing revision in general
plans, refinements of details, and new ideas of peripheral
 improvements, continued steadily until late in 1846,
at which point it was abandoned for just over ten years, and
then resumed for the remainder of Babbage's life. The
reasons for this hiatus and the character of the later
work on the Analytical Engine will be discussed in the
next chapter.
improvements, continued steadily until late in 1846,
at which point it was abandoned for just over ten years, and
then resumed for the remainder of Babbage's life. The
reasons for this hiatus and the character of the later
work on the Analytical Engine will be discussed in the
next chapter.
FOOTNOTES
#1
S.B., "Vol. XV," p. 101, referring to the Analytical Engine.
#2
B.C.E.. p. 212.
#3
See B.C.E.. pp, 264-69.
#4
See Chapter Two.
#5
B.C.E., p. 220. The property of the even differences of
the sine function which Babbage discussed is simply a
generalization of the property of its second difference
already described above.
#6
B.C.E., pp. 216-19.
#7
B.C.E., p. 216.
#8
B.C.E.. pp. 216-19.
#9
Transactions of the Cambridge Philosophical Society. Vol.
III (1824), p. 218.
#10
Reprinted in B.C.E., pp. 225-31.
#11
This volume (henceforth G.S.B.) is related to, but not
directly part of, the series of regular Scribbling Books at
South Kensington. Two pages spreads will be indicated by
the first line number on the verso sheet.
#12
G.S.B., 1. 1231.
#13
G.S.B., 1. 1261.
#14
B.C.E., pp. 268, 331. Apparently the only use of this
phrase by Babbage at the time was in the outline of a
paper to be called "Philosophy of the Calculating Engine,"
dated August 30, 1834 (Buxton, Vol. VII); this paper was
not written.
#15
The first sketch of the circular arrangement is at G.S.B.,
1. 1801; the sketch is not dated, but the next page has
the date September 18, 1834.
#16
This account is from Babbage's paper "The Analytical Engine,"
p. 9, dated November 8, 1869; Buxton, Vol. VII.
#17
This account was reconstructed from very vague material
in the vicinity of G.S.B., 1. 1801.
#18
Nowhere is any coherent account of this development
given by Babbage, and it has been pieced together from
scattered material, mostly in G.S.B. and S.B., Vol. I and Vol.
II, plus the drawings from the period. Specific references
will be given when possible. Note that S.B., Vol. I is
sometimes wrongly called Vol. XIII (see Bibliography).
#19
G.S.B., 1. 1861.
#20
See S.B., Vol. I, pp. 175-167 (working backward) and
S.K., Drawings II, 5-7 (this refers to the large drawings
in the South Kensington collection, in this case numbers
five through seven from Case II. See Bibliography on
numbering of drawings).
#21
G.S.B. 1. 1861 and S.B., Vol. I, pp. 175-167.
#22
G.S.B., 1. 1891.
#23
S.K., Drawing II, 14.
#24
G.S.B., 1. 1891.
#25
S.B., Vol. I, p. 172; S.K., Drawing II, 3.
#26
S.B., Vol. I. pp. 175. 4; S.K., Drawing II, 4.
#27
On the following, see especially S.B., Vol. I, pp. 30-31,
and G.S.B., 1. 1951, 1981. 2011, and 2301.
#28
See, e.g., S.K., Drawings II, 9 and 16.
#29
First notes on barrels and platforms; S.B., Vol. I,
pp. 14-21, February 26, 1835.
#30
S.B., Vol. I, pp. 140-41.
#31
S.K., Drawings II, 29 and 35. .
#32
S.B., Vol. I, p. 40.
#33
S.B., Vol..I, pp. 167-165.
#34
S.B., Vol. I, p. 165.
#35
Reprinted in B.C.E., p. 5.
#36
S.B.. Vol. I, p. 163.
#37
S.B., Vol, I, pp. 119-123.
#38
S.B., Vol. II, p. 19.
#39
S.B., Vol. II, p. 45.
#40
P.L.P., p. 126.
#41
First mention: S.B., Vol. II, p. 146; cf. Vol. I, p. 160.
#42
Curiously, Jacquard (1752-1854) had gotten the idea for
his loom from an earlier one made by Jacques de Vaueanson,
which he came across while rummaging among some old material
at the Conservatoire des Arts et Metiers in Paris. See
W.H.G. Armytage,A Social History of Engineering (Cambridge,
Mass.. 1961), p. 110: John Timbs, Stories of Inventors and
Discoverers (London, 1863), pp. 236-38.
#43
S.B., Vol. II, p. 150.
#44
Buxton, Vol. VII. Unfortunately the Buxton papers are
in considerable disarray, and the pages of this paper
are not all in order or even together. However, it can be
reconstructed in full.
#45
References will be given here to the short title
"Powers," with page numbers from Babbage's manuscript.
#46
"Powers," pp. 9-11. Note the limitations imposed by
the inflexible treatment of the decimal point, in contrast
with the exponential representation in current computers.
This is one reason Babbage provided what seems like a very
excessive number of wheels per column, since this did not
in general yield nearly as many significant digits as it
would seem.
#47
"Powers," p. 44.
#48
"Powers," pp. 12-13, S.B., Vol. III, p. 93.
#49
"Powers," p. 14.
#50
"Powers," p. 15.
#51
The relation of a barrel to its reducing apparatus
and to the rest of the machine can be seen in Figure 2;
also shown is the operation of a variable card. The
barrels could also be affected by the counting apparatus.
See also S.B., Vol. IV, p. 144.
#52
The preceding section on the Mill is all from "Powers,"
p. 2-8.
#53
"Powers," p. 40.
#54
"Powers," p. 21.
#55
"Powers," pp. 24-26.
#56
"Powers," pp. 32-36.
#57
Adapted from one by Henry P. Babbage; see B.C.E., p. 338.
#58
"Powers," p. 27.
#59
"Powers,", pp. 27-28.
#60
Ibid.
#61
"Powers," p. 23.
#62
See "Powers," pp. 31-32, 37, 46-53.
#63
"Powers," p. 50.
#64
S.B., Vol. III, p. 17 from back.
#65
"Powers," p. 15.
#66
S.B., Vol. IV, p. 385.
#67
B.M., Vol. VII..ff..525-29.
#68
B.M., Vol. VIII, ff. 292-93.
#69
Held by the Burndy Library, in Norwalk, Connecticut.
#70
MS. pp. 3-4.
#71
MS. pp. 8-9.
#72
"Powers," p. 53.
#73
"Powers," p. 19. It is interesting to compare this
passage with similar ones in recent works on computers. A
good example will be found in Faster then Thought, ed. B.V.
Bowden (New York, 1953), p. 29.
#74
Although he was also writing the Ninth Bridgewater
Treatise in 1837, and doing very extensive railway experiments
in 1839, among other things.
#75
B.M.. Vol. X. f. 67.
#76
B.M., Vol. X, ff. 287-89.
#77
Ibid.
#78
B.M., Vol. X, f. 246.
#79
P.L.P., p. 129.
#80
B.M., Vol. X, f. 582.
#81
Menabrea, 1809-1896, was an engineer and mathematician;
he later served as a general in the Italian army and as
prime minister from 1867-69; he became Marquis of Valdora.
#82
P.L.P., p. 130. for quotations above and below.
#83
B.M., Vol. X, f. 582.
#84
B.M., Vol. X, f. 638 this draft is not dated, but
internal evidence places it somewhat before August 12, 1841.
#85
It is capitalized on B.M., Vol. X, f. 645.
#86
See Chapter Two.
#87
B.M., Vol. X, f. 645.
#88
Buxton, Vol. VII.
#89
Ibid.
#90
Ibid.
#91
Vol. XLI, New Series, pp. 352-376.
#92
Vol. III, pp. 666-731.
#93
B.M., Vol. X, ff. 532-33
#94
Charles Babbage to Ada Augusta Lovelace, June 30, 1843;
in the Lovelace. Papers. Quoted in Maboth Moseley,
Irascible Genius (London, 1964), p. 169.
#95
Mosely, Irascible Genius, is the prime example, devoting
over a quarter of her biography of Babbage to material on
Lady Lovelace. Moseley is also convinced that Babbage
served for many years as an intermediary between Lady
Lovelace and the bookmakers to whom she became deeply and
scandalously in debt, and that the generally quite trivial
correspondence between her and Babbage involved some
phantasmagorical secret code concerning this illicit
activity; however, Moseley presents absolutely no
serious evidence for this (See Mosely, Chapter 22,
esp. p. 196).
#96
B.C.E., pp. 19-20; the paper and notes are reprinted in
B.C.E., pp. 4-50.
#97
B.C.E., p. 25.
#98
B.C.E., p. 44.
#99
P.L.P., pp. 135-36.
#100
See, for example, some of the amazingly arrogant remarks
quoted in Moseley, Irascible Genius, Chapter 20.
#101
B,M,, Vol. XI, ff. 407-9.
#102
B.M., Vol. XI, ff. 422-27.
#103
B.M., Vol. II, ff. 205-6. It is not clear just what
the papers were.
#104
B.M., Vol. XII, ff. 347-57.
#105
For date of change in emphasis, see S.B., Vol. III,
p. 68 from back. See also S.K., Notations 172 and 173,
dated November, 1840.
#106
S.B., Vol. III, pp. 368-70.
#107
S.B., Vol. III, pp. 374-77.
#108
"Powers," p. 27.
#109
At this point Babbage was considering thirty digits per
column as standard, rather than the earlier forty.
#110
S.B., Vol. IV, pp. 448-51, December 8-9, 1840.
#111
S.B., Vol. IV, p. 460.
#112
S.B., Vol. IV, p. 477.
#113
S.B.. Vol. IV, pp. 475, 501.
#114
S.B., Vol. IV, p. 482, January 3, 1841.
#115
S.B., Vol, V, p. 118, and S.K., Drawing II, 102.
#116
S.B., Vol. V, p. 132.
#117
S.B., Vol. V, pp. 183-89.
#118
S.B., Vol. VI, pp. 32-33.
#119
S.B., Drawing II, 136.
#120
S.B., Vol. III, pp. 161-66.
#121
S.B., Vol. III, pp. 75-76 from back.
#122
S.B., Vol. IV, p. 514. February 2, 1841.
#123
S.B., Vol. V, p. 389.
#124
S.B., Vol, V, pp. 454-59, 469-77, 533-34.
#125
Such as the program to compute Bernoulli numbers,
described in Note G to the Menabrea paper, B.C.E., pp. 45-50.
This was written by Babbage, not Lady Lovelace: see
P.L.P., P. 136.
#126
S.B., Vol. III, p. 90.
#127
S.B., Vol. III, pp. 88-89.
#128
S.B., Vol. III, p. 93.
#129
S.B., Vol. III, p. 100.
#130
S.B., Vol. V, p. 152.
#131
P.L.P. p. 122. Compare Babbage's The Exposition of 1851.
(London, 1851), pp. 185-87, where the ability of the
Engine to reject wrong cards was given as an example of
an apparently impossible power Babbage had given it,
without the method being explained. The same mystification
is attempted with the fact that the Engine could be made so
that wheels being turned by hand at any time would not cause
errors. Cf. S.B., Vol. V, pp. 334-35, January 28, 1843.
#132
"Powers," pp. 41-43; P.L.P., p. 119.
#133
S.B., Vol. V, p. 545, October 29, 1844.
#134
S.B., Vol. V, p. 322, January 11, 1843
#135
S.B., Vol. IV, pp. 216-18, September 21, 1839.
Preface
Chapter 1
Chapter 2
Chapter 3
Chapter 4
Chapter 5
 In order to understand the genesis of the Analytical
Engine, one must trace it back to 1822, to the first
stages of Babbage's work on the Difference Engine. As
mentioned in Chapter Two, Babbage had from the beginning
the idea of a machine to calculate tables by difference
methods for functions without a constant difference, and
he announced this idea in his "Letter to Sir Humphrey
Davy" in July, 1822.
2
It was out of this seed, which lay
dormant until 1834, that the Analytical Engine grew.
In order to understand the genesis of the Analytical
Engine, one must trace it back to 1822, to the first
stages of Babbage's work on the Difference Engine. As
mentioned in Chapter Two, Babbage had from the beginning
the idea of a machine to calculate tables by difference
methods for functions without a constant difference, and
he announced this idea in his "Letter to Sir Humphrey
Davy" in July, 1822.
2
It was out of this seed, which lay
dormant until 1834, that the Analytical Engine grew.